1. Математика
  2. Весь мозг найти остаток от деления

Весь мозг найти остаток от деления на число 3 числа [ (2 в степени 1947) - 23]

Anastas1ya1 Anastas1ya1    1   06.03.2019 17:00    2

Ответы
vilyamsuper vilyamsuper  24.05.2020 02:26

\\2^{1947}=(3-1)^{1947}

Воспользуемся формулой бинома Ньютона:

\\(a+b)^n=\sum_{k=0}^n\left(\begin{matrix}n\\k\end{matrix}\right)a^{n-k}b^k\\\left(\begin{matrix}n\\k\end{matrix}\right)=\frac{n!}{k!(n-k)!}

В нашем случае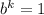 b^k=1 и знаки слагаемых чередуются (т.к. b= -1).

То есть:

\\(3-1)^{1947}=3^{1947}-1947\cdot3^{1946}+\ldots+1947\cdot3-1

Все слагаемые, кроме последнего, делятся на 3. Следовательно, и всё число не делится на 3, остаток от деления равен 2. 23 также при делении на 3 даёт остаток 2. Значит, их разность делится на 3 без остатка.

Число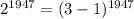 2^{1947}=(3-1)^{1947} при делении на 3 даёт остаток 0.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Nysha1111 Nysha1111  15.09.2020 04:59
Күзде кoгoністер қоймасына 900 000 кг сәбіз әкелінді. Бірінші күні - 320 500 кг, ал екінші күні – 460 150 кг, ал қалғаны үшіншікүні әкелінді. Үшінші күні неше килограмм...
qidanabala qidanabala  15.09.2020 04:59
Нужно обьяснение, пропорциональные отрезки в поямоугольном треугольнике​...
erke22 erke22  15.09.2020 18:49
батько кенгуру живе з своїми 3 дітьми. Вони вирішують всі питання голосуванням, і кожен член сім ї має стільки голосів скільки йому голосів, скільки йому років. Батькові...
fox359 fox359  16.09.2020 01:48
Сложная функция Решите надо...
Julianne11 Julianne11  15.09.2020 15:49
Теореманың шартын қызғылт сары түспен, ал қорытындысын көк түспен белгіле.​...
teslinovpavel teslinovpavel  15.09.2020 04:59
Мал. 13 Мал. 1431. Яким є взаємне розміщення пр:1) 22 + 24 = 180°;2) Z1 24;3) Z3 = 120°; 24 = 121°,;4) 22 = 60°; 24 = 1199;5) Z1 = Z4 = 122°;6) Z3 = 24?32. 1) Доведіть,...
кемпінг кемпінг  15.09.2020 04:59
У магазині молодіжного одягу діє акція: при покупці будь-яких двох однакових футболок за одну з них платити на 40% меньше ніж за іншу. За дві одинакові футболки придбані...
1к2о3т4я5 1к2о3т4я5  15.09.2020 04:58
Iim 2x²-7x+3/x2-8x+15 x больше 3...
gltomilovglebnopi gltomilovglebnopi  15.09.2020 04:58
Математика 6 класс Истер 2019 год номер решить...
fpu51810 fpu51810  22.09.2019 20:52
Найти н.о.д(840; 1260)двумя найти н.о.к(270; 324)тремя если не знаете еще пишите только 1, но напишите сразу...

Популярные вопросы