Верным выражением для полного дифференциала dz функции z=f(x,y) является
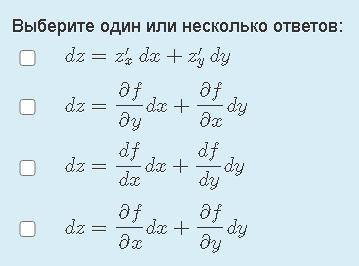
Другие вопросы по теме Математика
Популярные вопросы
- Почему сказка Гауфа холодное сердце актуальна в наши дни?...
2 - ПО ФИЗИКЕ КОНТРОЛЬНАЯ И САМОСТОЯТЕЛЬНАЯ РАБОТА 3, 7, 8, 9. ...
1 - Заполни пропуски модальными глаголами can,could,be able to в необходимой форме...
1 - Какие изменения в жизни Франции внесла декларация прав человека и гражданина...
3 - определите количество теплоты, необходимое для того, чтобы воду массой 20 граммов...
1 - Немецкий! Перекласти речення на німецьку мову, використовуючи минулий час Präteritum....
1 - Какое событие в 16 веке вы считаете наиболее важным для России...
2 - У Лизы было 5 спичек и она сложила их на столе так, что получилось три прямоугольника....
2 - Верны ли следующие утверждения? А. Водные растения не обитают на большой глубине,...
1 - Высота гранатового дерева равна 3 м.К вечеру длина его тени становится равной...
1
3,4
Пошаговое объяснение:
Эти ответы одинаковые, поэтому можно выбрать или два, или один из этих
Полный дифференциал dz функции z=f(x,y) определяется следующим образом:
dz = ∂z/∂x * dx + ∂z/∂y * dy,
где ∂z/∂x и ∂z/∂y обозначают частные производные от функции z по переменным x и y соответственно, а dx и dy - это малые приращения переменных x и y.
Теперь, рассмотрим предложенные варианты:
1) dz = ∂z/∂x * dx + ∂z/∂y * dy + ∂z/∂y = ∂z/∂x * dx + 2∂z/∂y * dy - ∂z/∂y.
Здесь, третье слагаемое ∂z/∂y верное, так как это частная производная относительно y. Однако, второе слагаемое 2∂z/∂y * dy не верное. Полный дифференциал не должен иметь коэффициент, отличный от 1, перед переменной dy.
2) dz = ∂z/∂x * dx + ∂z/∂y * dy + ∂z/∂y.
Здесь, третье слагаемое ∂z/∂y верное, так как это частная производная относительно y. Однако, полный дифференциал не может быть записан без слагаемого, содержащего dx. Поэтому, это выражение также неверно.
3) dz = ∂z/∂x * dx + ∂z/∂y * dy.
Это верное выражение для полного дифференциала dz функции z=f(x,y). Здесь, ∂z/∂x и ∂z/∂y представляют частные производные от функции z по переменным x и y соответственно, а dx и dy представляют малые изменения переменных x и y.
Таким образом, верным выражением для полного дифференциала dz функции z=f(x,y) является dz = ∂z/∂x * dx + ∂z/∂y * dy.