Велосипедист выехал с постоянной скоростью из пункта А в пункт В ,расстояние между которыми равно 204 км. Обратно он двигался

Question

Математика: Велосипедист выехал с постоянной скоростью из пункта А в пункт В ,расстояние между которыми равно 204 км. Обратно он двигался со скоростью на 5км/ч больше прежней . По дороге на обратном пути он сделал остановку на 5 часов. В результате он затратил на обратный путь столько же времени ,сколько на путь из А в В . Найти скорость велосипедиста на обратном пути .

alinadudocka · Answer

Пусть велосипедист сначала ехал из A в B со скоростью за время .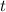

Тогда обратно он ехал со скоростью (v+5) за время, на 5 часов меньшее (ведь 5 часов он стоял, не двигался), то есть (t-5) .

Приравняем условия:

$vt=(v+5)(t-5)\\vt=vt+5t-5v-25\\5t-5v-25=0\\t-v-5=0\\t=v+5$

Вспоминаем условие о расстоянии:

$vt=204\\v(v+5)=204\\v^2+5v-204=0\\D=25-4 \cdot (-204)=841\\\sqrt{D}=\sqrt{841}=29\\v_1=\dfrac{-5+29}{2}=\dfrac{24}{2}=12\\v_2=\dfrac{-5-29}{2}=\dfrac{-34}{2}=-17.$

Второй корень не подходит, ибо скорость есть величина положительная ;)

Вспоминаем, что обратно он ехал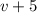 v+5 км/ч, то есть 12+5=17.

ответ: 17 км/ч. На скриншоте проверка на компьютере.

P. S. Решить эту задачу можно и не вводя вторую переменную (времени), но я так привык. При решении сложных задач, а не таких, несколько переменных более наглядны. С одной переменной было бы как-то так:

$\dfrac{204}{v}-5=\dfrac{204}{v+5}$

Можешь сам дорешать этим путём.

Велосипедист выехал с постоянной скоростью из пункта А в пункт В ,расстояние между которыми равно 20

Популярные вопросы