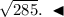вектор а=(2;3;-4); вектор б= вектор i+вектор j+ вектор k. Найти | 3а вектор + 2 б вектор
Другие вопросы по теме Математика
Популярные вопросы
- Согласны ли вы с утверждением, что большинство комплексов нашей планеты...
2 - Лидер мировой экономики: Китай; США; Япония...
1 - Укажите реку, в русле которой сформировалась дельта: 1) Обь; 2) Муррей;...
3 - Известный ученый океанолог В.Н. Степанов писал: «Вполне справедливо иногда...
1 - Области высотной поясности занимают самую большую площадь на материке:...
3 - Нарисуйте схему смены высотных поясов в горах, если у их подножия простираются...
2 - Какой материк пересекается экватором и нулевым меридианом? 1) Африка;...
3 - Где в основном сконцентрированы в Северной Атлантике запасы промысловых...
2 - Средняя глубина Мирового океана составляет: 100 м; 500 м; 3700 м; 11022...
1 - Самый маленький по площади океан: 1) Атлантический; 2) Тихий; 3) Индийский...
2
Дано: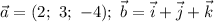
Найти: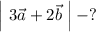
Решение. Вектор, представленный в пространстве в виде суммы единичных векторов (орт), то есть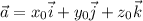 , где
, где 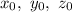 — числа, которые называются координатами вектора
— числа, которые называются координатами вектора 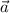 в некотором базисе, можно записать так:
в некотором базисе, можно записать так: 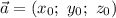
Таким образом,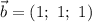
Умножение вектора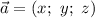 на число
на число 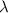 имеет вид:
имеет вид: 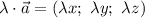
Таким образом,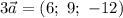 и
и 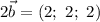
Для векторов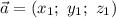 и
и 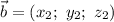 имеет место
имеет место 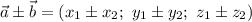
Таким образом,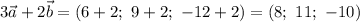
Длина вектора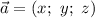 определяется как арифметический квадратный корень из суммы квадратов координат
определяется как арифметический квадратный корень из суммы квадратов координат 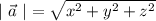
Таким образом,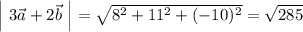
ответ: