Важно, ! там не сложно, но у меня нет времени делать,более того, варианты ответа есть. надеюсь на вас

Ответы

Mratom1111 01.10.2020 10:01

Пошаговое объяснение:

9. а) (берем производную, от констант она 0, от (x+2)/2 производная равна коэффициенту при х, т.е. 1/2)

10. M(X) =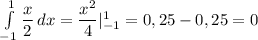 $\int\limits^1_{-1} {\dfrac{x}{2} } \, dx =\dfrac{x^2}{4} |_{-1}^1=0,25-0,25=0$

ответ: а)

11. D(X) = M(X²) - (M(X))² = M(X²) - 0 = M(X²)

M(X²) =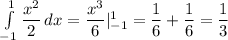 $\int\limits^1_{-1} {\dfrac{x^2}{2} } \, dx =\dfrac{x^3}{6} |_{-1}^1=\dfrac{1}{6} +\dfrac{1}{6}=\dfrac{1}{3}$

ответ: б)

ПОКАЗАТЬ ОТВЕТЫ

Hdhfr 01.10.2020 10:01

9. а) производную, от константы равна нулю, и от нуля и от единицы; а от (x+2)/2 производная равна (1+0)/2=1/2, верный ответ а)

10. M(X) =определенный интеграл от минус до плюс единицы от (1/2)*х4дх, и равен он х²/4, подставим пределы, получим 1/4-1/4=0, верный ответ а)

11. D(X) =∫x²f(x)дх(интеграл от минус единицы до плюс единицы) -(M(X))² =

1/3-0=1/3

((1/3)*∫x²дх=х³/6. (интеграл определенный, от минус до плюс единицы, у меня нет возможности ставить нижний верхний пределы, не забудьте поставить и равен интеграл 1/6-(-1/6)=2/6=1/3)

=2/6=1/3 ,верный ответ: б)

ПОКАЗАТЬ ОТВЕТЫ

Другие вопросы по теме Математика