Вася выписывает в ряд различные натуральные числа и следит за тем, чтобы любые 9 вы- писанных чисел имели общий делитель, больший единицы, а никакие 10 выписанных чисел такого общего делителя не имели (пока чисел меньше 9, на них ограничений нет). Докажите, что в какой-то момент Вася не сможет выписать очередное число.
Другие вопросы по теме Математика
Популярные вопросы
- Сумма двух углов равнобедренной трапеции равна 138° надите больший угол...
2 - Выбери и прочитай слово со звуком i . kite, bit , kod, fin, mope, home,...
2 - Хотябы 4 , чем раньше , тем лучше, жду ответа...
2 - Найдите значение выражения 4 4/33 + 3 8/33 2) 5 13/18 - 2 7/18 3) 23/48-14/58+5/48...
1 - Из 27 учеников класса 15 занимаются спортом,а 18 музыкой. некоторые из...
3 - какие слова являются жаргонизмами велик(велосипед) кардиология стукач...
2 - Зеленой+бумаги+купили+в+5+раз+большечем+красной+.+сколько+листов+бумаги+каждого+цвета+купилиесли+зеленой+больше+на+60+листов.++чем+красной...
1 - Скорость голубя 1800м в секунду можно ли догнать голубя на мошине которая...
1 - Составить предложение на казахском языке ( 5-6 предложений ) со словами...
3 - Last weekend was my mom s anniversary and we had a family got hering....
3
Предположим противное, то есть то, что Вася всегда сможет выписать очередное число. В силу попарного различия выписываемых чисел, их множество неограниченно.
Рассмотрим первые 9 чисел. Пусть у них есть общий делитель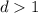 . Заменим теперь последнее число (9-ое в последовательности) на 10-ое в последовательности. Чисел снова 9 и у них должен быть общий делитель
. Заменим теперь последнее число (9-ое в последовательности) на 10-ое в последовательности. Чисел снова 9 и у них должен быть общий делитель 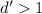 . Если при этом
. Если при этом 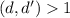 , то можно взять первые 10 чисел и у них окажется общий делитель
, то можно взять первые 10 чисел и у них окажется общий делитель 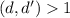 , противоречие. Значит,
, противоречие. Значит, 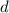 и
и 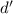 взаимно просты. Далее заменяем 10-ое число на 11-ое и так далее. Получаем бесконечное множество чисел, поскольку они попарно взаимно просты. Но все эти числа делят первые 8 чисел множества, у которых множество делителей, очевидно, ограничено. Противоречие. Следовательно, в какой-то момент Вася не сможет выписать очередное число.
взаимно просты. Далее заменяем 10-ое число на 11-ое и так далее. Получаем бесконечное множество чисел, поскольку они попарно взаимно просты. Но все эти числа делят первые 8 чисел множества, у которых множество делителей, очевидно, ограничено. Противоречие. Следовательно, в какой-то момент Вася не сможет выписать очередное число.