Вариант 1 Б
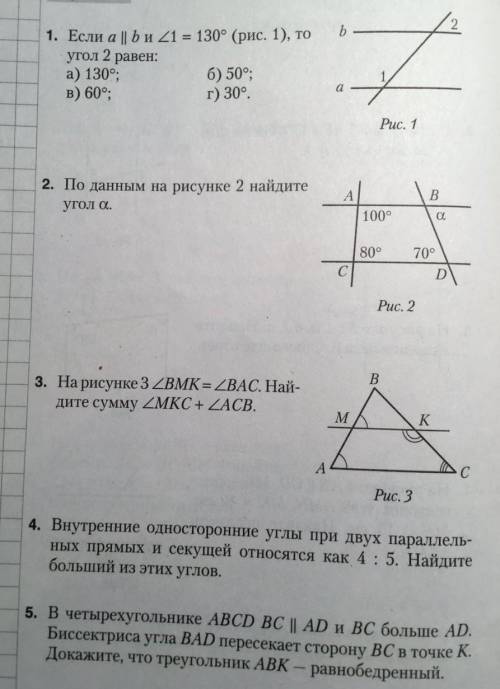
1. Если а|| Би 21 = 130° (рис. 1), то
угол 2 равен:
а) 130°;
6) 50;
в) 60°;
г) 30°,
Рис. 1
2. По данным на рисунке 2 найдите
угол а.
100
С
80
70
Рис. 2
B
3. На рисунке 3 ZBMK = 2ВАС. Най-
дите сумму ZMKC +ZACB.
K
С
Рис. 3
4. Внутренние односторонние углы при двух параллель-
ных прямых и секущей относятся как 4: 5. Найдите
больший из этих углов.
5. В четырехугольнике ABCD BC || AD и BC больше AD.
Биссектриса угла BAD пересекает сторону ВС в точке К.
Докажите, что треугольник ABK - равнобедренный.
64​

Вариант 1 Б

1. Если а|| Би 21 = 130° (рис. 1), то угол 2 равен:
а) 130°;
б) 50;
в) 60°;
г) 30°.

На рисунке 1 мы видим, что a и Би параллельны, и угол 21 равен 130°. Так как угол 2 и угол 21 образуют Z, а углы, возникающие при пересечении двух параллельных прямых линий с третьей прямой, называемой трансверсальной, одинаковы, то угол 2 также равен 130°. Ответ: а) 130°.

2. По данным на рисунке 2 найдите угол а.

На рисунке 2 у нас есть две параллельные прямые С и В, а также секущая прямая АБ. Угол между секущей прямой и прямой В обозначен символом а. Угол в прямоугольном треугольнике ACB равен 90°. Так как углы, образованные при пересечении двух параллельных прямых с третьей, одинаковы (по теореме о соответственных углах), то угол С равен 90°.

Угол а и угол С образуют линию, поэтому их сумма равна 180°. Получаем уравнение:
а + 90° = 180°
а = 180° - 90°
а = 90°

Ответ: угол а равен 90°.

3. На рисунке 3 ZBMK = 2ВАС. Найдите сумму ZMKC + ZACB.

На рисунке 3 у нас есть две параллельные прямые ZC и BM. Угол ZBMK равен углу 2ВАС и состоит из двух равных углов.

Сумма углов ZMKC и ZACB равна углу ZBMK, так как они образуют одну фигуру - ZBMK.
Таким образом, сумма углов ZMKC и ZACB равна (2ВАС + 2ВАС) = 4ВАС.

Ответ: сумма углов ZMKC и ZACB равна 4ВАС.

4. Внутренние односторонние углы при двух параллельных прямых и секущей относятся как 4:5. Найдите больший из этих углов.

По условию задачи, внутренние односторонние углы при двух параллельных прямых (назовем их А и В) и секущей прямой (назовем ее С) относятся как 4:5.

Предположим, что больший угол - это угол, образованный прямыми А и С. Обозначим его как угол ∠1. Тогда меньший угол будет углом, образованным прямыми В и С, и обозначаемый как угол ∠2.

Согласно условию задачи, соотношение углов должно быть 4:5, то есть:
∠1/∠2 = 4/5

Мы можем представить это соотношение как уравнение:
4х = 5х - 1 (где х - это мера углов ∠1 и ∠2, х является общим множителем)

Решаем уравнение:
4х - 5х = -1
-х = -1
х = 1

Таким образом, мера каждого угла (∠1 и ∠2) равна 1. Из условия задачи нам нужно найти больший угол, поэтому ответ - это мера угла ∠1, равная 1.

Ответ: больший угол равен 1.

5. В четырехугольнике ABCD BC || AD и BC больше AD. Биссектриса угла BAD пересекает сторону ВС в точке К. Докажите, что треугольник ABK - равнобедренный.

Доказательство:

Данный вопрос требует доказательства, что треугольник ABK является равнобедренным. Для этого нам необходимо показать, что стороны АК и ВК равны друг другу.

У нас есть следующие данные:
- BC параллельна AD и BC больше AD
- Биссектриса угла BAD (это линия, которая делит угол BAD пополам) пересекает сторону ВС в точке К.

Из этих данных следует, что углы BAK и KAD равны, так как они являются вертикальными и, следовательно, имеют одинаковую меру.

Также, по теореме о соответственных углах, угол BAK и угол KAD равны.

Итак, у нас есть две пары углов, которые равны друг другу. Таким образом, треугольник ABK является равнобедренным, так как у него две равные стороны (АК и ВК) и два равных угла (BAK и KAD).

Доказательство завершено. Треугольник ABK - равнобедренный.