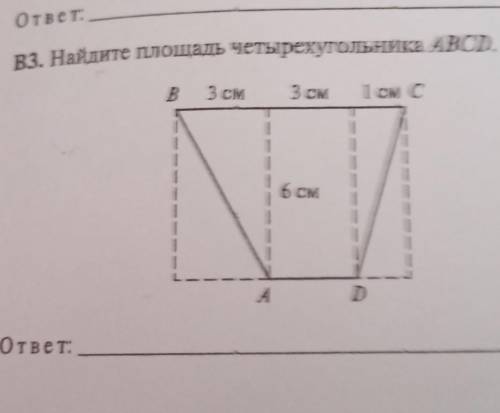
В3. Найдите площадь четырехугольника ABCD. B
3 см
1 см с
3 см
І
| 6 см
А
D
ответ:​

Перед нами трапеция. Площадь трапеции равна произведению высоты и половине суммы оснований

Добрый день!

Для того, чтобы найти площадь четырехугольника ABCD, нам понадобится разделить его на два треугольника и просуммировать их площади.

Обратимся к изображению и обозначим точки E и F на стороне BC таким образом:

- Точка E будет делить сторону BC в отношении 3:1, то есть на отрезке BE будет 3 см, а на отрезке EC будет 1 см.
- Точка F будет делить сторону CD в отношении 1:3, то есть на отрезке CF будет 3 см, а на отрезке FD будет 1 см.

Теперь, чтобы найти площадь треугольника ABE, нам понадобятся его высота и основание.

Основание треугольника ABE составляет сторона AB между точками A и B, то есть 6 см.

Высоту треугольника ABE можно найти, проведя отрезок EF параллельно стороне AB и соединив точку пересечения этого отрезка с AB, которую мы обозначим как H. Точка H является высотой треугольника ABE.

Поскольку отрезок EF параллелен стороне AB и имеет общую точку с нею (точку E), то говорится, что EF является опоясывающим гранью треугольника ABE.

Таким образом, площадь треугольника ABE можно найти, умножив его основание AB на высоту AH.

Основание AB равняется 6 см, а высоту AH можно найти, измерив расстояние между отрезками AB и EF. Оно будет равно 3 см, поскольку EF делит сторону AB в отношении 3:1.

Итак, площадь треугольника ABE равна 6 см (основание) умножить на 3 см (высота), что дает 18 квадратных сантиметров.

Аналогично, мы можем найти площадь треугольника DCF.

Основание треугольника DCF равняется отрезку CD, то есть 6 см.

Высоту треугольника DCF можно найти, измерив расстояние между отрезками CD и EF. Оно будет равно 1 см, поскольку EF делит сторону CD в отношении 1:3.

Итак, площадь треугольника DCF равна 6 см (основание) умножить на 1 см (высота), что дает 6 квадратных сантиметров.

Наконец, чтобы найти площадь четырехугольника ABCD, мы сложим площади треугольников ABE и DCF.

18 квадратных сантиметров + 6 квадратных сантиметров = 24 квадратных сантиметра.

Итак, площадь четырехугольника ABCD равна 24 квадратных сантиметра.