В задачах 41 – 50 даны координаты точек

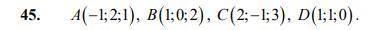
Другие вопросы по теме Математика
Популярные вопросы
- написать сочинение не большое но и не очень короткое по картине Февральская...
1 - Определите нок чисел, предварительно выписав множества простых множителей...
3 - .Доберіть синоніми до слів бігти та йти ,складіть і запишіть з ними речення...
2 - 5 предложений в страдательном залоге...
3 - Дана арифметическая прогрессия (ан). Известно, что a1 = 7 и d = 4. Подсчитайте...
3 - Реакція кисня з речовинами з виділенням тепла і світла називається? А)...
3 - Шлях від абсолютизму до парламентської монархії в Англії...
2 - 677. бөлігі бойынша шамаларды табыңдар: 16 м; 4) 8. 12 т; 7) 2 і 4 сағ:і...
3 - Знайдіть міру кута дванадцятикутника...
1 - 238. Дополните предложения недостающими словами. Запишите их. Приведите...
1
Даны вершины треугольной пирамиды:
A (-1; 2; 1), B(1; 0; 2), C(2; -1; 3), D(1; 1; 0).
Найти:1) длину ребра АВ.
Вектор АВ= (1-(-1); 0-2; 2-1) = (2; -2; 1), его модуль равен √(4+4+1) = √9 = 3.
2) уравнение плоскости грани ABC.
Находим нормальный вектор n как векторное произведение АВ и АС.
Вектор AB: (2; -2; 1), вектор АС: (3; -3; 2).
n = ABxAC =
I j k| I j
2 -2 1| 2 -2
3 -3 2| 3 -3 = -4i + 3j - 6k- 4j + 3i + 6k = -1i – 1j + 0k.
Нормальный вектор плоскости АВС равен n =(-1; -1; 0).
Уравнение плоскости АВС по точке A (-1; 2; 1) и нормальному вектору n =(-1; -1; 0):
ABC: (-1)*(x + 1) – 1* (y – 2) + 0*(z – 1) = 0,
ABC: -x – y + 1 = 0.
3) уравнение перпендикуляра DO из точки D на плоскость АВС по направляющему вектору n =(-1; -1; 0) и точке D(1; 1; 0):
DO: (x – 1)/(-1) = (y – 1)/(-1).
4) площадь грани АВС найдём как половину модуля векторного произведения АВхАС.
S(ABC) = (1/2) )√((-1)² + (-1)² + 0²) = √2/2 = 0,707 кв.ед.
5) объем пирамиды ABCD.
A (-1; 2; 1), D(1; 1; 0), ABxAC = =(-1; -1; 0).
Вектор AD = (2; -1; -1).
V = (1/6)|AD*( ABxAC)| = (1/6)*|2*(-1) + (-1)*(-1) + (-1)*0| = 1/6 ≈ 0,16667 куб.ед.