В задачах 11 – 20 дана невырожденная матрица A. Найти обратную матрицу A-1 и пользуясь правилом умножения матриц, показать, что A * A-1 = E ,где E –единичная матрица.
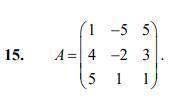
Другие вопросы по теме Математика
Популярные вопросы
- Назовите признаки попадания инфекции в рану...
3 - Назови элемент и найди число электронов, недостающих до завершения его внешнего...
2 - Підготуйте невелику інформацію Образи майбутнього у творах сучасного мистецтва...
3 - Все приведённые ниже характеристики кроме двух используют для описания методов...
2 - Если в ответе десятичная дробь, то запишите её через запятую. Если в ответе обыкновенная...
1 - 1 Укажите сложное предложение с сочинительной и подчинительной связью. Скудные...
3 - 8. Приведите пример субъекта России с высокой долей населения старше 65 лет..9....
1 - Если в ответе десятичная дробь, то запишите её через запятую. Если в ответе обыкновенная...
2 - Виберіть слова та словосполучення, які стосуються міського життя за литовськопольської...
3 - 1. Реалистическое и романтическое изображение войны в рассказах сборника «Морская...
3
Пошаговое объяснение:
Сначала найдем определитель этой матрицы.
Как его искать, я расписывать не буду, вы сами должны знать.
|A| = 1(-2)*1 + 4*1*5 + 5(-5)*3 - 5(-2)*5 - 4(-5)*1 - 1*1*3 =
= -2 + 20 - 75 + 50 + 20 - 3 = 10
Определитель не равен 0, значит, обратная матрица существует.
Теперь находим миноры.
Составляем матрицу алгебраических дополнений:
Я поменял знаки у тех миноров, у которых сумма индексов нечетна, то есть у M(1,2), M(2,1), M(2,3), M(3,2)
Транспонированная матрица алгебраических дополнений:
Обратная матрица:
Всё!