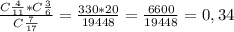. В ящике находится 11 стандартных и 6 бракованных деталей (всего 17 деталей). Наудачу и без возвращения вынимают 7 деталей. Найти вероятность того, что будет выбрано ровно 4 стандартных и 3 бракованных детали.
Другие вопросы по теме Математика
Популярные вопросы
- Составить предложения с этими интонации...
1 - Это с/! ❤️❤️❤️ твір-роздум: чи існують гобсеки у сучасному суспільстві?...
1 - Cоставить план по теме ,,рынок 4 пункта плана, два которых развернуто(не менее...
3 - Оцените с точки зрения складывающейся демографической ситуации каждую из ,...
1 - Используя mmo описать образование молекулы f2 какой ион является донором в...
1 - F(x)= (x-2) (6+x) / (x-1) ^ найти точки максимума и минимума функции...
1 - Когда и каким образом арабам удалось значительную часть пиренейского полуострова?...
2 - Из 32 учебник 9 класс ладыженская выписать примеры на согласование,премыкание,....
1 - Доведіть що максим і мирослава із твору про захара беркута сміливі та мужні...
3 - I. завдання з вибором однієї правильної відповіді . 1. фразеологія вивчає...
2
Пошаговое объяснение:
Комбинации выбора стандартных деталей :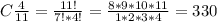
Комбинации выбора бракованных деталей: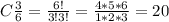
Всего выбор любых деталей: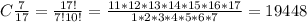
Вероятность будет равна P=