В треугольнике mnp отрезок EF параллелен MP, KF параллелен MN, угол fkp=54° Найти область четырёхугольника MEFK
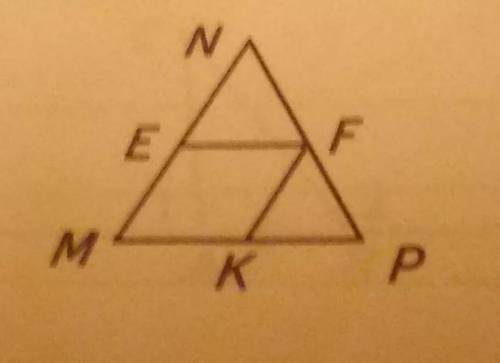
Другие вопросы по теме Математика
Популярные вопросы
- Укажите падеж прилагательных: знойного; августовских; тёплых; красноголовые;...
3 - Методы политической борьбы 16-17 века в нидерландах...
2 - Решите уровнение 5х+3/9=27/13,5. 8/20=28/9х+7...
3 - Выскажи мнение: можно ли лёгкие отнести к органам выделения?...
2 - Как построить какой-нибудь четырехугольник abcd у которого ab||cd и bc||ad...
3 - Звуко-буквений анализ слив: джмелi-дзвонарi, дзвоники....
2 - Как вы считаете какие слова являются омонимами а какие антонимами...
2 - Транскрипція: безсовісний суджено качається зжовкнути...
3 - На основе данных примеров докажите,что и суффикс несёт информацию о лексическом...
2 - Заполните таблицу и докадите что,в египте возникла цивилизация....
3
Пошаговое объяснение:
1) Так как MN параллелен KF, то и ME (является частью стороны MN) параллелен KF. Аналогично, MK параллелен EF.
2) Признак параллелограмма: Если противоположные стороны четырёхугольника попарно параллельны, то четырёхугольник является параллелограммом. Действительно, исходя из первого шага, можно утверждать, что MEFK является параллелограммом.
3) Угол MKF и FKP являются смежными, значит их сумма равна 180. Найдём угол MKF:
∠MKF = 180 ° - ∠FKP = 180 - 54 =126°
4) Свойство: противоположные углы параллелограмма равны. Следует, что ∠MEF = ∠MKF = 126°
5) Свойство четырехугольника MEFK: сумма углов равна 360°, значит ∠MEF+∠EFK+∠MKF+∠KME=360°. Два угла нам известны:
126°+∠EFK+126°+∠KME=360
∠EFK+∠KME=108°
По свойству параллелограмма ∠EFK=∠KME, значит ∠EFK=∠KME=108 / 2 = 54°.