В трапеции ABCD BC=2см, BD=AD=7см. Найдите длину отрезка BO
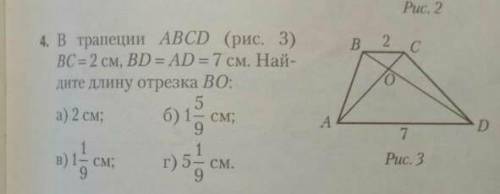
Другие вопросы по теме Математика
Популярные вопросы
- Что такое естественная убыль населения ?...
3 - Найти и выписать глаголы с орфограммой букв з(с) на конце приставок. подчеркнуть...
1 - Какие виды осуществлял на своем острове робинзон крузо?...
1 - Вслове обеспечьте мягкий знак в корне или в суффиксе?...
2 - 4человека обменялись сколько было всего...
3 - Составьте любую сказку или волшебную,бытовую или о животных.буду !...
2 - Составить предложения со словами зеркальце,крыльцо,кольцо...
3 - Мама дала детям 16 абрикос,4 сливы и 2 конфеты. сколько всего фруктов дала мама...
1 - Аднакараневыя словы к слову на узлеску...
2 - Леонардо да винчи — где дух не водит рукой художника, там нет искусства !...
2
1. Сумма длин двух противоположных сторон трапеции равна сумме длин оснований. В нашем случае, это AB + CD = BC + AD.
2. Линия, соединяющая середины параллельных сторон трапеции, параллельна основаниям и ее длина равна половине разности длин оснований. То есть BO = (AB - CD) / 2.
Используя эти факты, решим задачу пошагово:
Шаг 1:
Из условия задачи знаем, что BC = 2 см, BD = 7 см и AD = 7 см.
Шаг 2:
Применим первый факт о трапеции: AB + CD = BC + AD.
Заменяя известные значения, получим AB + CD = 2 + 7.
Упрощаем выражение: AB + CD = 9.
Шаг 3:
Применим второй факт о трапеции: BO = (AB - CD) / 2.
Заменяя значения, получим BO = (9 - CD) / 2.
Шаг 4:
На данной стадии нам не хватает информации о длине CD, поэтому нужно найти ее.
Воспользуемся теоремой Пифагора. Так как трапеция ABCD - прямоугольная трапеция, то применим эту теорему к треугольнику BCD.
BD^2 = BC^2 + CD^2.
Подставляем известные значения: 7^2 = 2^2 + CD^2.
Вычисляем: 49 = 4 + CD^2.
Затем вычитаем 4 из обеих сторон: 45 = CD^2.
Извлекаем квадратный корень обеих сторон: CD = √45.
Упрощаем выражение: CD = 3√5 см.
Шаг 5:
Теперь, когда мы знаем длину CD, мы можем найти длину BO.
Подставляем известные значения в формулу: BO = (9 - CD) / 2.
BO = (9 - 3√5) / 2.
Таким образом, длина отрезка BO составляет (9 - 3√5) / 2 см.