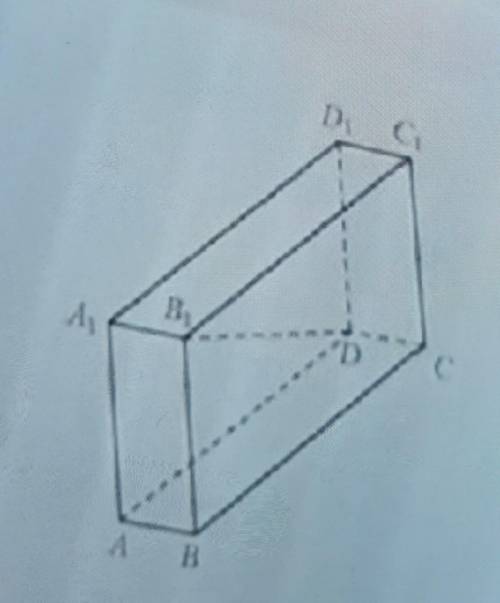
В прямоугольном параллелепипеде abcda1b1c1d1 известно, что cc1=4, ab=1, b1c1=8. Найти диагонали db1
Другие вопросы по теме Математика
Популярные вопросы
- Расположите бромиды щелочных металлов в порядке возрастания их температур...
2 - Вычислить плотность по водороду оксида азота no ) d(h2)=mr(no)/mr(h2)=15,...
2 - Какое количество нефти ( в тоннах) вмещает цилиндрическая цистерна...
3 - Вдоль берега морфологический разбор существительного...
1 - Если бы новая теория начисто отрицала сложившиеся знания, наука...
3 - Сколько электронов и протонов содержат: cr2o7( -2); no3(-1); nh4(+)...
3 - Прямоугольный треугольник с катетами 10 см и 24 см вращается вокруг...
2 - Площадь полной поверхности цилиндра 500π см². диаметр его основания...
3 - Написать критерии вида любого животного...
1 - Главная мысль сказки страшная коза ушинского...
1
Прямоугольный параллелепипед - это трехмерная геометрическая фигура, у которой все грани являются прямоугольниками.
В задаче используются следующие обозначения:
- a, b, c, d - вершины параллелепипеда
- a1, b1, c1, d1 - соответствующие вершины противоположной грани
Теперь давайте разберемся, что означают следующие данные:
- cc1 = 4 - это расстояние между вершинами c и c1. Важно заметить, что эти вершины находятся на противоположных гранях параллелепипеда.
- ab = 1 - это длина стороны ab параллелепипеда.
- b1c1 = 8 - это длина стороны b1c1 параллелепипеда.
Теперь перейдем к решению задачи.
Мы хотим найти диагонали db1 параллелепипеда.
Для начала построим рисунок, чтобы лучше понять геометрическую конфигурацию задачи.
В прямоугольном параллелепипеде abcda1b1c1d1 известно, что cc1 = 4, ab = 1 и b1c1 = 8.
c1______b1
/ /|
/ d1 / |
/_______ / |
| | |
| | |
| | |
a ____|_______ | /
| | | /
| | |/
| | |
d_____|_______b
Теперь рассмотрим прямоугольный треугольник db1c1.
Известно, что b1c1 = 8 и cc1 = 4.
Мы можем использовать теорему Пифагора, чтобы найти длину диагонали db1.
Теорема Пифагора гласит: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Применяя теорему Пифагора к треугольнику db1c1 получим:
db1^2 = dc1^2 + b1c1^2
Так как cc1 = 4, то и dc1 = 4.
Подставим значения:
db1^2 = 4^2 + 8^2
db1^2 = 16 + 64
db1^2 = 80
Теперь найдем квадратный корень из обеих сторон уравнения:
db1 = √80
Чтобы упростить ответ, разложим 80 на простые множители:
80 = 2 * 2 * 2 * 2 * 5
Теперь заметим, что у числа 80 есть квадраты 4 и 16. Корень из них мы можем извлечь:
√4 = 2
√16 = 4
Теперь выразим √80 через √4 и √16:
√80 = √(2 * 2 * 2 * 2 * 5)
√80 = 2 * 2 * √5
√80 = 4√5
Таким образом, ответ на задачу: диагональ db1 параллелепипеда равна 4√5 или примерно 8.94 (округлим до сотых).