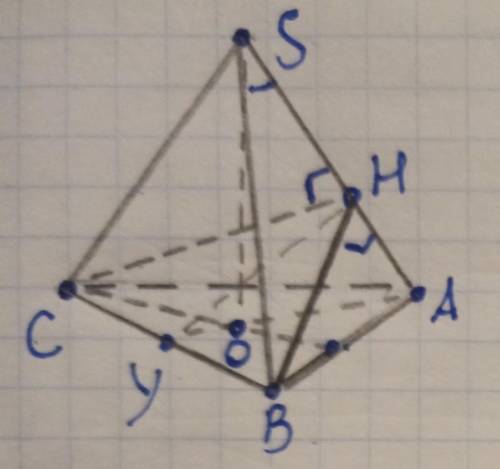
В правильной треугольной пирамиде sabc с вершиной s через сторону bc основания перпендикулярно ребру sa проведено сечение. плоский угол ребра равен 60. Высота пирамиды равна 2√2. Найдите площадь сечения.
Другие вопросы по теме Математика
Популярные вопросы
- Из чисел 24,576,345,970,538,4325,8211,1435,960,156120 выпишите те которые...
3 - Посмори на рисунок и закончи эти предложения пообразцу. 1) thet plane.where...
1 - Определите до какого разряда округление знач.велич 384000...
1 - Текст міркування гість у дім радість у нім...
3 - Сочинение на тему профессии изменившие названия...
1 - Мальчик в 1 ый день прочел 10 страниц, 2ой день-25 страниц,3ый день-40 страниц....
3 - Морфемный разбор слова ёршик...
1 - Романтик значение этого слова в толковом словаре...
3 - Как называется асфальтированная дорога...
3 - Разложите на простые множители : 2025, 3969, 13125....
3
У нас есть правильная треугольная пирамида sabc, где s - вершина пирамиды. Через сторону bc основания мы проводим сечение перпендикулярно ребру sa, образуя плоский угол равным 60 градусам. Высота пирамиды равна 2√2.
Для начала, давайте найдем длину ребра пирамиды (длину отрезка sa). Мы знаем, что угол ребра равен 60 градусам. В правильной треугольной пирамиде каждый угол основания равен 60 градусам. Так как у нас основание треугольное, то это означает, что у каждого угла треугольника основания равны 60 градусов.
Зная эти сведения, мы можем использовать теорему косинусов для треугольника sabc, чтобы найти длину ребра пирамиды. Обозначим длину ребра как a.
Теорема косинусов гласит:
a^2 = h^2 + b^2 - 2hb cos(60)
h - высота пирамиды, равная 2√2
b - длина основания треугольника, которая равна стороне bc в нашем случае.
Подставляем известные значения:
a^2 = (2√2)^2 + b^2 - 2 * 2√2 * b * cos(60)
a^2 = 8 + b^2 - 4√2b * 0.5
a^2 = 8 + b^2 - 2√2b
Так как треугольная пирамида правильная, каждая сторона треугольника основания равна a.
Теперь давайте рассмотрим сечение, которое проведено через сторону bc. Мы должны найти площадь этого сечения.
Поскольку пирамида правильная и сечение проведено перпендикулярно основанию, мы можем считать, что сечение представляет собой правильный треугольник.
Площадь правильного треугольника можно найти с помощью формулы:
площадь = (сторона^2 * √3) / 4
В нашем случае, сторона треугольника основания равна a. Подставим это значение:
площадь = (a^2 * √3) / 4
Используя значение a, которое мы нашли ранее, мы можем найти площадь сечения.
Место для дальнейшего решения (подставляются значения и возводятся в степень):
площадь = (8 + b^2 - 2√2b)^2 * √3 / 4