В правильной трёхгранной прямой пирамиде дана сторона основания A и боковое ребро B. Определите угол наклона апофемы боковой грани к основанию

Пошаговое объяснение:

1. Апофема - это высота боковой грани, в правильной пирамиде является также её медианой. Также по определению, основанием правильной пирамиды является правильный многоугольник (в данном случае треугольник), и у него равны все стороны.

2. Найти угол наклона апофемы мы можем через прямоугольный треугольник, в котором апофема - это гипотенуза, высота пирамиды - противолежащий катет (1), радиус вписанной в треугольник основания пирамиды окружности - прилежащий катет (2).

Радиус вписанной в правильный треугольник окружности (второй катет) равен 1/3 высоты или (сторона *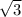 )/6 (тоже свойство правильного треугольника). То есть (A* 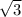)/6

Найдем, первый катет.

3.  Первый катет равен по теореме Пифагора корню из разности квадратов бокового ребра пирамиды (то есть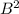 ) и радиуса описанной вокруг основания пирамиды окружности (по свойству правильного треугольника равного (сторона * * 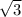)/3 или (A* 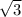)/3).

Первый катет = =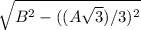

4. Искомый угол выражается через тангенс, то есть отношение противолежащего (первого) катета к прилежащему (второму) катету:

/

Упрощаем и получаем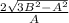 = tg искомого угла.