В правильной шестиугольной пирамиде SABCDEF сторона основания равна корень из 3, а боковое ребро равно 3. Найдите угол SAC. ответ дайте в градусах.
Другие вопросы по теме Математика
Популярные вопросы
- От глагола отрезать взять приставку,от прилагательного разговорчивый корень,от глагола...
3 - Будь ! придумати 5 реченнь на ійській мові з словами should, have to, need, can,...
2 - Найдите наименьшее общее кратное чисел 14 и 8...
1 - Придумай свою используя любые данные в текст или в таблице запиши её условие вопрос...
1 - Тридцать комариков(выбежали,выбегали)на поляну и заиграли на своих писклявых скрипках.как...
2 - Определите формулы пропущенных соединений в цепи: s- so2? - h2so3- nahso3- ?...
3 - Сколько изомерных кислот у бутановой кислоты? я нашла только одну(2-метилпропановая...
3 - Предложение с словом сахар для 3 класса...
3 - Высота ромба делит его сторону пополам. найдите меньший угол ромба. ....
2 - Замените сказуемые в предложениях глаголами синонимами. какой текст у вас получился...
2
В основании правильный шестиугольник, поэтому ∠ABC=120°.
Пусть BH⊥AC, H∈AC.
ΔABC равнобедренный (AB=BC=√3), поэтому BH - медиана и биссектриса. То есть ∠CBH=60°.
В прямоугольном треугольнике BHC (∠C=90°):
HC=BC·sin(∠CBH)=√3·√3/2=3/2
AH=HC=3/2
ΔASC равнобедренный (AS=SC=3). Раз H - середина AC, то SH высота треугольника ASC.
В прямоугольном треугольнике SHA (∠H=90°):
cos(∠SAH)=AH/SA=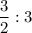 = 1/2 ⇒ ∠SAH=60°.
= 1/2 ⇒ ∠SAH=60°.
∠SAC=SAH как углы с одинаковыми сторонами.
ответ: 60.