1. Математика
  2. В правильной четырёхугольной

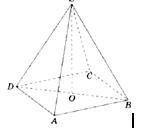
В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 16, ВD = 40. Найдите боковое ребро SC


В правильной четырёхугольной пирамиде SABCD точка О – центр основания, S – вершина, SО = 16, ВD = 40

Mara6458 Mara6458    1   23.12.2020 20:27    0

Ответы
1domrahev 1domrahev  22.01.2021 20:30

ответ: SC=4√16

SC=SA=SB=SD=40( по условию - пирамида правильная, значит все боковые рёбра равны)

Рассмотрим ΔSOB, так как пирамида правильная, то в основании квадрат, а BD- диагональ квадрата, Точка О- высота пирамиды делит диагональ пополам( ΔDSB- равнобедренный, SO- является высотой и медианой одновременно)

ОВ= BD:2=40:2=20

По теореме Пифагора найдём SB²=SO²+OB²

SB=\sqrt{16^2+20^2}=\sqrt{16*16+16*25} =\sqrt{16(16+25)} =\sqrt{16*41}=4\sqrt{16}

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Артём24532523 Артём24532523  13.09.2020 12:56
Выислите tg x/2, если cosx=0.4, pi...
ирина1523 ирина1523  13.09.2020 12:55
Ученик в тетради изобразил клетками план кварталов, каждый из которых имеет форму квадрата со стороной 39 мм. Ширина всех улиц в этом районе — 7 мм...
nik180208 nik180208  13.09.2020 12:55
складіть рівняння кола, центр якого знаходиться в точці М (1; -3) і яке проходить через точку B(-2; 5)...
Vftfg Vftfg  13.09.2020 12:55
Упрости выражение и найди его значение при d = 6,6. -7d(7d +7) + (7d - 7) (7 +7d). ответ:...
stenyakina90 stenyakina90  13.09.2020 12:54
знайдіть усі такі прості числа p, для яких p-1 має рівно 10 дільників, а число p+1 має рівно шість дільників...
sasha17210 sasha17210  13.09.2020 12:54
7/9*(6/7-9/14)= (5/6+5/9)*18/25= по действиям в столбик....
урааа28 урааа28  13.09.2020 12:54
3 -1 4 5||| 5 2 0 -1|||0 2 1 -3|||6 -2 9 8|||Вычислить определитель данной матрицы желательно методом понижения порядка​...
yaremhykv04 yaremhykv04  13.09.2020 12:52
F(x) и уравнения касательной, 11 класс умоляю, иначе мне конец...
1nVictUS 1nVictUS  13.09.2020 12:52
решить неравенства методом интервалов. Желательно написать на листочке и сфотать....
mafeei mafeei  13.09.2020 12:52
завтра тест нужно сделать сегодня!...

Популярные вопросы