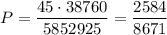В партии из 30 деталей – 20 деталей первого сорта и 10 – второго сорта. На проверку берут 8 деталей. Какова вероятность, что 2 из них будут
второго сорта?
Другие вопросы по теме Математика
Популярные вопросы
- Сталь массой 2 кг нагревается на 1000 градусов кузнечным горном. каков кпд кузнечного...
1 - Найдите нод чисел: в)60,80,48. б)195,156,260....
1 - Морфологический разбор слова 1)растет 2)нагреть...
3 - Периметр треугольника равен 51 см. отношение длины первой стороны к длине второй...
3 - Help, help, вычислите, сколько процентов составляет : 1) 4,2 от 6 4) 4,96 от 6,2...
2 - Почему у человека царство : животные...
3 - Найти значение букв в равенстве 768: 48-с: 48...
1 - Найдите вме простые делиьели числа 990,512,864...
1 - Является ли лейбл изобретателем капиталистического рынка?...
1 - Imagine you are famous person.everyone wants to take a photo with you or speak...
3
Общее число исходов равно числу вынуть из партии 8 деталей из 30, то есть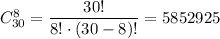 . Число благоприятных исходов: выбираем 2 детали второго сорта из 10, т.е.
. Число благоприятных исходов: выбираем 2 детали второго сорта из 10, т.е. 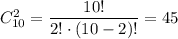 , а 6 деталей первого сорта из 20:
, а 6 деталей первого сорта из 20: 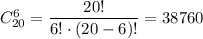 . По правилу произведения, итого
. По правилу произведения, итого 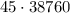
Искомая вероятность: