В основании прямой треугольной призмы лежит равнобедренный прямоугольный треугольник с гипотенузой 10 см. Найдите боковое ребро призмы, если ее боковая поверхность равна 200 см2.

см

Пошаговое объяснение:

Площадь боковой грани данной призмы будет равна гипотенузе основания, умноженной на высоту призмы, т.е. площадь этой грани равна 10h, где h - высота призмы Две остальных грани будут равны, т.к. лежат на равных катетах основания. Найдём, чему будет равен катет основания:

Площадь этих граней равна .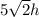

Площадь боковой поверхности равна сумме всех боковых граней. Выразим её через h.

Поскольку площадь боковой поверхности призмы равна 200, составим уравнение, откуда и найдём h: