1. Математика
  2. В окружности с центром О проведён

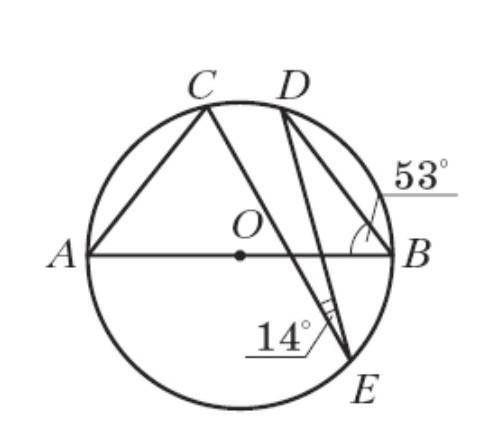
В окружности с центром О проведён диаметр АВ (рис.) Найдите угол CAB, если CED = 14°, ABD = 53 . ​


В окружности с центром О проведён диаметр АВ (рис.) Найдите угол CAB, если CED = 14°, ABD = 53 . ​

hopelless2124 hopelless2124    1   12.12.2020 05:58    75

Ответы
nadijagordijenp07vwr nadijagordijenp07vwr  18.01.2024 13:15
Для решения этой задачи мы воспользуемся свойством окружности, согласно которому угол, стоящий на полуокружности (угол, центральный по отношению к одной из ее дуг), равен 90 градусов.

Исходя из этого, рассмотрим треугольники АОС и BOC. Поскольку радиус окружности одинаков для всех точек, то он равен OA = OB = OC. Также мы знаем, что угол AOB составляет 180 градусов, поскольку это прямой угол (угол на диаметре). Из этого можно заключить, что треугольники АОС и BOC равнобедренные (две стороны равны - радиус и отрезки, соединяющие конец диаметра с точками на окружности).

Теперь вернемся к исходной задаче. У нас есть треугольник CAB, в котором нам нужно найти угол CAB. Мы знаем, что угол CED (угол, стоящий на полуокружности) равен 14 градусов. Поскольку CED и CAB - это вертикальные углы, они равны друг другу. Значит, угол CAB = 14 градусов.

В ответ на задачу "Найдите угол CAB, если CED = 14°, ABD = 53°", угол CAB равен 14 градусов.
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Yaroslav1RUS Yaroslav1RUS  19.05.2019 02:20
Кристина продает 8 стеклянных колокольчиков стоимостью 1 грн, 2 грн, 3 грн, 4 грн, 5 грн, 6 грн, 7 грн, 8 грн. сколькими кристина сможет разложить все эти колокольчики...
umarova5 umarova5  19.05.2019 02:20
№1 а)найдите нод(10668; 9810) б)сократите дробь 9810/10668 №2 а)найдите нод (1176; 1764) б)сократите дробь 1176/1764 №3 решите уравнение: 2(x - 2) + 3 = 0,4(x + 8)...
alexfeels555 alexfeels555  19.05.2019 02:20
Спростити вираз 2а*+2 – а+1 + 3а-3 а*-1 а-1 2а+2 * - це в другому степені...
katerinalavrenchuk katerinalavrenchuk  19.05.2019 02:20
Это не д/з но мне нужно! вопросы по теме о коми даны такие вопросы: 1.на что был похож космический корабль, который приземлился рядом с гришуней из сказки елены габовой?...
prisheplub prisheplub  19.05.2019 02:20
Плавательный бассейн наполняется двумя трубами при их совместной работе за 48 мин.через первую трубу бассейн может наполнится за 2 часа.за сколько времени наполнится бассейн...
kotovaann2016 kotovaann2016  19.05.2019 02:20
Как правильно перейти дорогу вблизи поворота дороги ?...
Ctatuetca Ctatuetca  19.05.2019 02:20
На овощную базу во второй день на 6,8 т арбуза больше, чем в первый день. сколько тонн арбуза на базу за два дня, если известно, что в первый день в 1,4 раза меньше арбуза,...
06Loki90 06Loki90  19.05.2019 02:20
Сколько существует натуральных чисел меньших 100? которые 1вариант-делятся одновременно на 2 и на 3 2вариант-делятся на 2 но не делятся на 3 3вариант-делятся на 3 но не...
тупой177 тупой177  19.05.2019 02:20
(участвуя в опросе, отвечайте на вопросы ответом, первым пришедшим в голову, желательно друг у друга не подглядывать) 1. что едят на завтрак? 2. что модно намылить? 3....
evolved evolved  19.05.2019 02:20
3,6+2,4: (11,7-3,7)= решите в столбик ответ будет 3,9 а я не могу понять как решить...

Популярные вопросы