В неколрой геометрической прогрессии b1+b2=51, a b2+b3=102. Найдите , 27 МИНУТ ОСТАЛОСЬ
Другие вопросы по теме Математика
Популярные вопросы
- Выделить в словах корень.листик,небесный.звёздочка.ножик.з...
1 - Запишите в виде обыкновенной дроби частное 2: 17 6: 19 22: 25...
2 - Во ско-ко раз 1а больше 1 кв.дм, 1га больше 1 кв. дм, 1 кв.км больше 1а, 1...
1 - Верно ли утверждение, что культура - это просвещенность, образованность, начитанность...
3 - На планете инопия живут инопики. у трех инопиков вместе 15 ручек и ножек,...
3 - Из пунктов а и б навстречу друг другу выехали автомобиль со скоростью 60 км/ч...
3 - Как бы я вел в чрезвычайной ситуации...
1 - Не пытайтесь угадать эти числа найдите p3+q3p3+q3, если известно, что p+q=6p+q=6...
1 - Напишите названия материков и больших островов...
1 - Укажите уравнение, соответствующее условию данной : из двух пунктов, расстояние...
3
Пусть чилса отличаются в k раз, то
b1=n
n+nk=51
nk+nk²=102
вычтем из второго уравнения первое:
сложим оба уравнения:
приравниваем оба уравнения с n и получаем, что первый знаменатель должен быть равен второму =>
корни по виета 2 и -1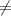 51)
51)
-1 не подходит(если подставить в первое уравнение n-n
подставляем двойку в первое уравнение, получаем:
3n=51 => n =17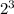 =136
=136
ну и четвертый член равен
17*