(в моих вопросах также есть другие нерешенные задания, буду благодарна, если заглянете))
Другие вопросы по теме Математика
Популярные вопросы
- Приведите примеры использования гальванических элементов и аккумуляторов...
1 - В чём состоит принципиальное отличие гальванического элемента от...
2 - Что значит объяснить графически написание наречий ?...
2 - Что собой представляет элемент Вольта?...
1 - Каков принцип работы гальванического элемента?...
3 - Два одинаковых лёгких шарика из фольги подвешены: один — на шёлковой...
3 - Заряженный электроскоп соединили палочкой с незаряженным (рис. 137)....
2 - Какая энергия может превращаться в источнике тока в электрическую?...
1 - Посмотрите внимательно на рисунок 136 и объясните принцип работы...
3 - Каково основное назначение источника тока? Приведите примеры известных...
3
Вначале сделаем некоторые упрощения (основные свойства корней и степеней, фактически никаких подсчетов):
А теперь можно либо посчитать, что находится под корнем, либо избежать муторных вычислений и сразу сказать, что числитель меньше знаменателя, и дробь меньше единицы. Значит, и корень из такой дроби тоже меньше единицы.
Итог: число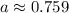 не подходит.
не подходит.
2). Второе число.Расписываю менее подробно:
Очевидно, что знаменатель в подкоренном выражении меньше единицы, поэтому само подкоренное выражение больше единицы. И корень больше единицы.
Итог: число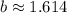 подходит.
подходит.
3). Третье число.
И, наконец, последнее число:
Здесь, опять, подкоренное выражение больше единицы (по вполне понятным причинам), так что и сам корень будет больше единицы.
Итог: число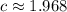 подходит.
подходит.
ответ: b и c.