В квадратном ковре на рисунке имеется 21 белый квадрат, а остальная часть площади ковра черная. Какая часть площади ковра- чёрная?

Другие вопросы по теме Математика
Популярные вопросы
- Составьте формулы трех солей азотной кислоты и трех солей сероводородной...
3 - Начерти прямоугольник у которого стороны 4 см и 3 см. найди периметр...
1 - Решите уровнение х + 3/4 =11/10 20...
3 - Впервой ёмкости на 3 л воды больше, чем во второй. если из первой...
2 - Какие отношения называются межличностными? в чем состоят их основные...
3 - Какая часть речи слов всегда ивысоко...
1 - При каких значениях х дробь не имеет смысла 4/x-2...
2 - Вырози величины в десятичных дробях: а)в метрах: 15 дм, 15 см,...
2 - Чем занимается архетиктурная акустика...
2 - Рівняння за схeмою kmno4 o2 al2o3...
1
Пошаговое объяснение:
Пусть сторона всего ковра равна 1 (при изменении этого значения соотношения не изменятся). Тогда она равна шести диагоналям маленького белого квадрата, откуда диагональ маленького белого квадрата равна , а сторона —
, а сторона — 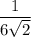 , значит, площадь —
, значит, площадь — 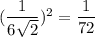 .
.
Сторона большого белого квадрата — сторона ковра без двух диагоналей маленького белого квадрата, то есть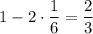 , его площадь —
, его площадь —  .
.
Площадь чёрной части ковра — это площадь всего ковра без белых квадратов: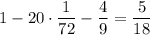 .
.