В квадрат, сторона которого равна 32 см, вписан другой квадрат, вершины которого являются серединами сторон первого квадрата, в этот квадрат вписан таким же образом другой квадрат, и т. д. (см. рис.).

Найди сумму площадей всех квадратов.

Дополнительные во сторона третьего по порядку квадрата равна...
2. Площадь наибольшего квадрата равна...
3. Знаменатель равен...

В основной квадрат (со стороной 32см) вписывается бесконечное количество последующих квадратов, сторона которых равна половине диагонали предыдущего.

Площадь первого равна 32*32 = 1024

Площадь второго равна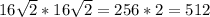

Замечаем, что это убывающая геометрическая прогрессия , знаменатель которой равен 1/2

Сумму площадей всех последующих квадратов можно посчитать по формуле суммы бесконечно убывающей геом. прогрессии

сторона третьего квадрата равна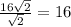 единиц

Наибольший квадрат - первый, и его площадь равна 32*32 = 1024 кв.ед

Знаменатель геом. прогрессии равен 1/2 или 0,5