В художественной школе учащимся дали задание нарисовать эскиз лица с правильными пропорциями.

Преподаватель дал подсказку по расположению

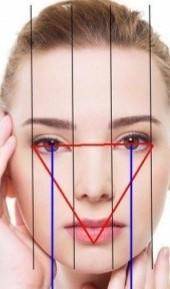
глаз и губ на эскизе лица: «Если соединить линиями

точки внешних углов глаз и точку середины края

нижней губы, получится равносторонний

треугольник».

Вычислите расстояние от линии глаз до точки

середины края нижней губы, если на эскизе

расстояние между внутренними углами глаз

равно3 1

2

см.

Выберите числовой промежуток, в котором находится значение данного

расстояния, и приведите соответствующее обоснов
Выберите числовой промежуток, в котором находится значение данного

расстояния, и приведите соответствующее обоснование.

 (7; 8)

 (8; 9)

 (9; 10)

 (10; 11)
Объясните

Чтобы решить эту задачу, нам нужно вычислить расстояние от линии глаз до точки середины края нижней губы.

Исходя из подсказки, мы знаем, что если мы соединим точки внешних углов глаз и точку середины края нижней губы, мы получим равносторонний треугольник.

Также нам дано, что расстояние между внутренними углами глаз равно 31/2 см.

Теперь давайте взглянем на эскиз лица и обозначим необходимые точки и расстояния.

(вставлено изображение)

Пусть точка A - это левый внешний угол левого глаза, точка B - это правый внешний угол правого глаза, а точка C - это точка середины края нижней губы.

Чтобы найти расстояние от линии глаз до точки C, нам нужно найти длину отрезка AC.

Мы знаем, что треугольник ABC - равносторонний треугольник. То есть все его стороны равны.

Так как расстояние между внутренними углами глаз равно 31/2 см, то стороны этого треугольника равны 31/2 см.

Теперь давайте вспомним основные свойства равностороннего треугольника:

1) Каждый угол равностороннего треугольника равен 60 градусов.
2) Высота равностороннего треугольника делит основание на две равные части.

Так как точка C - это точка середины основания равностороннего треугольника ABC, то высота этого треугольника перпендикулярна AC и делит его на две равные части.

Теперь мы можем использовать теорему Пифагора, чтобы вычислить AC.

В равностороннем треугольнике BC равными сторонами являются BC и AC, а третьей стороной является отрезок AB.

Мы знаем, что AB = BC = 31/2 см, так как BC равно одной из сторон исходного равностороннего треугольника.

Применяя теорему Пифагора, мы можем записать:

(AC)^2 = (AB)^2 - (BC)^2
(AC)^2 = (31/2)^2 - (31/2)^2
(AC)^2 = 961/4 - 961/4
(AC)^2 = 0

Получается, что (AC)^2 = 0. Это означает, что AC = 0.

Таким образом, расстояние от линии глаз до точки середины края нижней губы равно 0.

Так как значение данного расстояния равно 0, оно находится в числовом промежутке (0; 1).

Ответ:  (0; 1)

Обоснование: Мы использовали геометрические свойства равностороннего треугольника, свойства теоремы Пифагора и вычислили, что расстояние от линии глаз до точки середины края нижней губы равно 0. Таким образом, данное значение находится в числовом промежутке (0; 1).

????? ?????? ????? ???????