В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 билетов. Определить вероятность того, что среди обладателей билетов окажутся

Question

Математика: В группе из 25 студентов, среди которых 10 девушек, разыгрываются 5 билетов. Определить вероятность того, что среди обладателей билетов окажутся две девушки.

orazaymesaurov · Answer

Пусть событие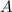 — две девушки обладают билетом. Тогда нужно найти вероятность того, что двумя билетами будут обладать девушки, а тремя — юноши.

Всевозможными комбинациями выбора 5 билетов из 25 студентов: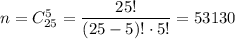 $n = C^{5}_{25} = \dfrac{25!}{(25-5)! \cdot 5!} = 53130$

Выбор билетов для 2-х девушек из 10: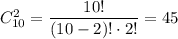 $C^{2}_{10} = \dfrac{10!}{(10-2)! \cdot 2!} = 45$

Выбор билетов для 3-х юношей из 15: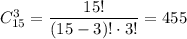 $C^{3}_{15} = \dfrac{15!}{(15-3)! \cdot 3!} = 455$

Тогда количество выбора 5 билетов для 2-х девушек и 3-х юношей можно определить, используя правило комбинаторного произведения: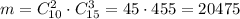 $m = C^{2}_{10} \cdot C^{3}_{15} = 45 \cdot 455 = 20475$ .