В 7^А классе учится 20 человек, и все они очень любят многопользовательские компьютерные игры. Каждый из учащихся играет в одну или две таких игры. При этом для любых 2 учащихся найдется общая игра (в которую играют оба). Найдите наибольшее N, такое, что гарантированно найдется игра, в которую играют не менее N учащихся.
Другие вопросы по теме Математика
Популярные вопросы
- Сколько будет 7x уможить (8-2x умножить (16+32x)=0 найдите значение...
2 - Периметр параллелограмма равен 40. одна сторона параллелограмма на...
3 - Вам ! в совсем любой книге откройте страницу 95.3 строчку в верху.что...
3 - Напиши о своем любимом животном. воспользуйся планом: my favorite...
2 - Определить расстояние между петропавловск и астана...
3 - Сочинение на тему семья моего друга...
3 - 1, меньшая сторона прямоугольника равна 4 см и образует с диагональю...
3 - Найдите величину 1)10÷ от 80 и; 100л...
3 - Составь программу действий и вычисли. 32 +8 ×(49 ÷7) - (40÷5 +27)÷5...
2 - Определить расстояние между жезказган и семей...
2
Пусть - число учащихся, которые играют в игру
- число учащихся, которые играют в игру  . Нужно отсортировать игры в порядке возрастания
. Нужно отсортировать игры в порядке возрастания  . Тогда мы можем получить следующую систему неравенств:
. Тогда мы можем получить следующую систему неравенств:
Где - наибольший индекс, такой что
- наибольший индекс, такой что 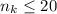 . В этой системе неравенств
. В этой системе неравенств  является наибольшим возможным числом учащихся, которые играют в одну из игр
является наибольшим возможным числом учащихся, которые играют в одну из игр  , а
, а 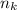 - число учащихся, которые играют только в игру
- число учащихся, которые играют только в игру  . Таким образом, наибольшее число
. Таким образом, наибольшее число  учащихся, которые играют в одну игру, равно
учащихся, которые играют в одну игру, равно  . Наша задача - найти наибольшее возможное значение
. Наша задача - найти наибольшее возможное значение  .
.
По условию, для любых двух учащихся найдется общая игра. Это означает, что для любой пары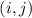 ,
,  , выполняется условие
, выполняется условие 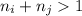 . Также из условия
. Также из условия  следует, что для любой пары
следует, что для любой пары 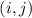 ,
, 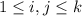 , выполняется условие
, выполняется условие 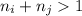 . Если мы присвоим значение
. Если мы присвоим значение 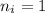 всем играм
всем играм  , то условия выше будут выполнены, но сумма
, то условия выше будут выполнены, но сумма 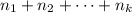 будет меньше
будет меньше  . Поэтому мы можем заметить, что если
. Поэтому мы можем заметить, что если 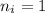 для некоторых
для некоторых  , то сумма
, то сумма 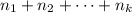 будет меньше
будет меньше  . Отсюда следует, что все игры
. Отсюда следует, что все игры  имеют
имеют  . Таким образом, наибольшее число учащихся, которые играют в одну игру, равно
. Таким образом, наибольшее число учащихся, которые играют в одну игру, равно  . Поскольку это число должно быть меньше
. Поскольку это число должно быть меньше  , то
, то 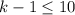 , что означает, что
, что означает, что  . Значит, наибольшее число
. Значит, наибольшее число  учащихся, которые играют в одну игру, равно
учащихся, которые играют в одну игру, равно  , где
, где  - наибольший индекс, такой что
- наибольший индекс, такой что 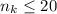 . Значит, наибольшее число
. Значит, наибольшее число  учащихся, которые играют в одну игру, равно
учащихся, которые играют в одну игру, равно  .
.
ответ: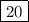 .
.
Наибольшее число N, при котором гарантированно существует игра, в которую играют не менее N студентов, равно 20. Это объясняется тем, что если каждый студент играет в одну или две игры, и для любых двух студентов есть общая игра, то каждый студент должен играть хотя бы в одну игру, которая является общей для всех 20 студентов в классе. Поэтому наибольшее число N, при котором гарантированно найдется игра, в которую играют не менее N учеников, равно 20.