Уважаемые МОЗГи! Задание, достойное Вас Найти общее решение линейного однородного уравнения с пере">
Другие вопросы по теме Математика
Популярные вопросы
- Какое животное с половым диморфизмом?...
2 - Множество всех первообразных функции y=5x имеет вид...
1 - Придумать какую-нибудь неважно просто просто...
3 - Лист бумаги сложили пополам, потом еще пополам и так 6 раз,...
3 - Какие опасные явления за рекой белой? ?...
2 - Обьясните тему приближение десятичных дробей , сегодня контрольная...
1 - Как можно охранять реку белую от загрязнений?...
2 - Напиши ответ автору письма, которое тебе больше всего понравилось....
3 - Как найти синус угла если известен его тангенс?...
1 - Вычислите 25/28-18/35, 40/63-35/72, 22/21-21/22...
2
1)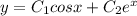
2)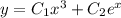
Пошаговое объяснение:
ЛОДУ 2ого порядка с переменными коэффициентами имеет вид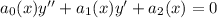
Общее решение такого ДУ - линейная комбинация двух его линейно независимых частных решений.
В обоих заданиях необходимо заметить, что сумма коэффициентов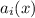 равна 0. Значит, очевидно, одним из частных решений данного ДУ будет функция
равна 0. Значит, очевидно, одним из частных решений данного ДУ будет функция 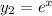 [и действительно:
[и действительно: 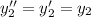 , а тогда уравнение принимает вид
, а тогда уравнение принимает вид 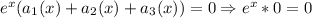 - верное равенство].
- верное равенство].
1) Рассмотрим Вронскиан системы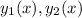 :
:
Значит, данные частные решения линейно независимы - а тогда общее решение имеет вид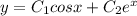 .
.
2) Очевидно искать частное решение в виде многочлена. Пусть его старший член равен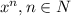 [коэффициент при старшей степени не имеет значения, т.к. уравнение однородное], т.е.
[коэффициент при старшей степени не имеет значения, т.к. уравнение однородное], т.е. 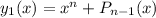 .
.
Тогда
То есть коэффициент при старшей степени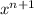 получаемого в левой части многочлена равен
получаемого в левой части многочлена равен  [степень
[степень 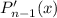 не выше
не выше 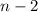 , а
, а 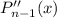 не выше
не выше 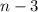 ]. Но в правой части тождественный ноль - а значит если некий многочлен и является частным решением уравнения, то это многочлен степени 3.
]. Но в правой части тождественный ноль - а значит если некий многочлен и является частным решением уравнения, то это многочлен степени 3.
Нетрудной подстановкой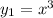 убеждаемся, что это решение ДУ:
убеждаемся, что это решение ДУ:
А тогда общее решение имеет вид