Уважаемые МОЗГи! Задание, достойное Вас Найти общее решение уравнения методом неизвестных коэффици">

1) y''-3y'

Решение уравнения будем искать в виде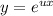 . Составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами.

Тогда систему составят функции:        

Общее решение однородного уравнения: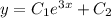 , где C ∈ R

2) 2ch3x

Ищем частное решение

R(x) и S(x) это полиномы, их степень - макс. степень полиномов P(x) и Q(x)

У нас:                    

Поэтому k у нас равен 1 (т.к. 0i наш корень кратности)

И уравнение имеет частное решение

y=x(Ax+B)

Находим производные, которые нужно подставить в исходное ур.

Отсюда получаем систему, приравняв коэф. при х:

Решаем и находим корни: A=0, B=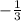

Тогда частное решение примет вид: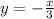

И теперь общее решение уравнения примет вид:

Второе решается АНАЛОГИЧНО! Пояснять решения далее не буду, все расписал в 1 примере

1)y''-3y'

2) 16ch4x

k у нас равен 1

Система;

Корни:

Вид частного решения: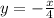

И теперь общее решение уравнения примет вид: