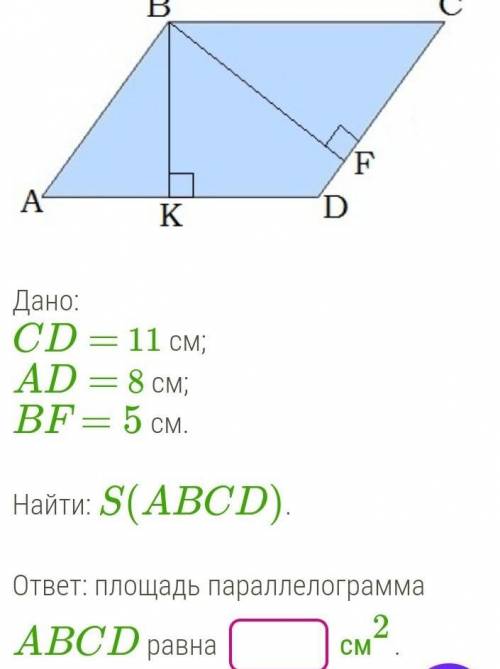
Условие задания: В
с
F
А
K
D
Дано:
CD = 11 см;
AD = 8 см;
BF= 5 CM.
-
.
Найти: S(ABCD)
ответ: Площадь параллелограмма
2
ABCD равна
См
CANAL​

Для решения задачи, нам необходимо узнать площадь параллелограмма ABCD.

Сначала определим высоту параллелограмма. Высота - это отрезок, проведенный из вершины D (или C) перпендикулярно стороне AB (или BC). Для этого нарисуем отрезок DH, перпендикулярный стороне AB, где H - точка пересечения DH и AB.

Теперь у нас есть два прямоугольных треугольника: треугольник АDH и треугольник BCH. Мы знаем, что сторона AD равна 8 см, сторона CD равна 11 см, а сторона BF равна 5 см. Задача состоит в определении высоты.

Применим теорему Пифагора для треугольника АDH:
(AD)^2 + (DH)^2 = (AH)^2.

Мы знаем, что AD = 8 см, поэтому:
8^2 + (DH)^2 = (AH)^2.

Теперь рассмотрим треугольник BCH, применим теорему Пифагора:
(BF)^2 + (CH)^2 = (BH)^2.

Мы знаем, что BF = 5 см, поэтому:
5^2 + (CH)^2 = (BH)^2.

Мы знаем, что сумма сторон двух противоположных сторон параллелограмма равна (CD + AB).
Следовательно, AB + CD = BC (или AD + BC = AB).

Мы знаем, что AD = 8 см, CD = 11 см, поэтому:
8 + BC = AB.

Теперь у нас есть система уравнений:
8^2 + (DH)^2 = (AH)^2,
5^2 + (CH)^2 = (BH)^2,
8 + BC = AB.

Решим эту систему уравнений.

Найдем высоту DH:
Субституируем DH из уравнения (8 + BC = AB) в уравнение (8^2 + (DH)^2 = (AH)^2):
8^2 + ((8 + BC) - AB)^2 = (AH)^2.

Теперь рассмотрим треугольник BCH, применим теорему Пифагора:
5^2 + (CH)^2 = ((8 + BC) - AB)^2.

Мы знаем, что BC = AB - 8, поэтому:
5^2 + (CH)^2 = (AB - 8)^2.

У нас есть два уравнения:
8^2 + ((8 + BC) - AB)^2 = (AH)^2 и 5^2 + (CH)^2 = (AB - 8)^2.

Теперь решим систему этих двух уравнений, чтобы найти высоту параллелограмма.
Подставим (AB - 8) вместо BC в первом уравнении:
8^2 + ((8 + (AB - 8)) - AB)^2 = (AH)^2.

Разрешим скобки:
8^2 + (AB - AB)^2 = (AH)^2.

Упростим выражение:
8^2 + 0^2 = (AH)^2.

Решением данного уравнения получаем:
(8 + 0) = (AH)^2,
AH = 8.

То есть высота параллелограмма равна 8 см.

Теперь найдем площадь параллелограмма, используя формулу:
S(ABCD) = AB * DH.

У нас уже есть значения AB = 8 + BC и DH = 8 см.
Подставим значения:
S(ABCD) = (8 + BC) * 8.

Мы знаем, что AB + CD = BC, поэтому:
S(ABCD) = (8 + AB - 8) * 8,
S(ABCD) = AB * 8.

Мы также знаем, что AB = 8 + BC, поэтому:
S(ABCD) = (8 + BC) * 8.

Теперь заменим BC на значение (AB - 8):
S(ABCD) = (8 + (AB - 8)) * 8.

Упростим выражение:
S(ABCD) = AB * 8,
S(ABCD) = 8 * AB.

Таким образом, площадь параллелограмма ABCD равна 8 умножить на AB.

Ответ: Площадь параллелограмма ABCD равна 8 умножить на AB (S(ABCD) = 8 * AB) или в данном случае "См".