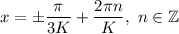Уравнение с параметром К:
cosКx=1/2
Другие вопросы по теме Математика
Популярные вопросы
- Заполни примеры.458+678+727+769=821+951+723+298+744=...
3 - Сочинение. тема я вас любил (лирика а.с.пушкин)...
1 - Решите уравнение -3 меньше 2 х -9 меньше или равно 1...
2 - Расставить знаки арифметических действий 300 20 10 4 =154...
3 - Написать сочинение рассуждение по тексту рябинка рябинка выросла рябинка при дороге....
1 - Поразмышляйте, крещение руси - это результат государственного подхода князя владимира...
2 - Фенологические наступления времени года в саратове....
1 - На каких путях предполагал николай решение крестьянского вопроса? какие меры в...
3 - Скажите,,почему i gonna think? (i m going),а почему просто нельзя сказать i m...
2 - Решите уравнения -3 меньше 2 х- 9 меньше или равно 1...
1
Если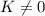 , то обе части последнего равенства разделим на
, то обе части последнего равенства разделим на 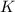 :
:
Заметим, что если , то исходное уравнение примет вид:
, то исходное уравнение примет вид:
Но так как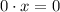 при любых значених
при любых значених  , а
, а  , то левая часть не может принимать значение
, то левая часть не может принимать значение  .
.
Значит, при уравнение не имеет решений.
уравнение не имеет решений.
ответ: при : нет решений;
: нет решений;
при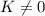 :
: