Уравнение геометрического места точек на плоскости ХОУ, равноудаленных от точек А (2;-3) и В (-4;1), имеет вид Выберите один ответ:
3х-2у-1=0
2у-3х+1=0
3х+2у+1=0
3х-2у+1=0
3х+2у-1=0

Ответы

рустамммм 06.08.2021 09:08

$y = \frac{3}{2}x + \frac{1}{2}$ или $x = -\frac{1}{3} + \frac{2}{3}y$

Пошаговое объяснение:

Нам нужно составить уравнение геометрического места точек на плоскости ОXY равноудаленных от точек с координатами A (2; -3) и B (-4; 1).

Решать задачу будем следующим образом:

вспомним формулу для нахождения расстояния между точками на плоскости;

обозначим точки равноудаленные от А и В координатами (x; y);

запишем расстояния между точкой А и (x; y);

запишем расстояние между точками B и (x; y);

приравняем расстояния и выразим одну переменную через другую.

Вспомним формулу для нахождения расстояния на плоскости

Формула для нахождения расстояния между точками на плоскости выглядит так:

AB =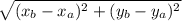 $\sqrt{(x_b - x_a)^2 + (y_b - y_a)^2}$ , где точки А и В заданы координатами A и B

Формулу мы вспомнили, теперь можем записать расстояние между точками А с координатами (2; -3) и (x; y) и точками B с координатами (-4; 1) и (x; y).

Составим уравнение геометрического места точек

Записываем расстояние между точкой A (2; -3) и (x; y):

$\sqrt{(x - 2)^2 + (y - (-3))^2}$ ;

Записываем расстояние между точками B (-4; 1) и (x; y):

$\sqrt{(x - (-4))^2 + (y - 1)^2}$ ;

Так как геометрического места точек на плоскости ОXY равноудаленных от точек A и B мы приравниваем полученные выражения:

$\sqrt{(x - 2)^2 + (y - (-3))^2} = \sqrt{(x - (-4))^2 + (y - 1)^2}$ ;

(x - 2)^2 + (y - (-3))^2 = (x - (-4))^2 + (y - 1)^2 ;

Открываем скобки, переносим все слагаемые в право и приводим подобные.

x^2 - 4x + 4 + y^2 + 6y + 9 = x^2 + 8x + 16 + y^2 - 2y + 1

-4x+4+6y +9-8x-16+2y-1=0 ;

-12x-4+8y=0

$x = -\frac{1}{3} + \frac{2}{3}y$

или

$y = \frac{3}{2}x + \frac{1}{2}$ .

ПОКАЗАТЬ ОТВЕТЫ

лох249 06.08.2021 09:08

ответ: №4 .

Геометрическим местом точек, равноудалённых от концов отрезка АВ, является серединный перпендикуляр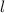 этого отрезка , проходящий через точку М .

$A(2;-3)\ ,\ B(-4;1)\\\\seredina\ AB:\ \ tochka\ M\Big(\dfrac{2-4}{2}\ ;\ \dfrac{-3+1}{2}\Big)\ \ ,\ \ \ M(-1;-1)\\\\\overline{AB}=(-6;4)\ \ ,\ \ \vec{s}\parallel \overline{AB}\ \ \to \ \ \ \vec{s}=(-3;2)\ \ \Rightarrow \\\\\vec{n}=(2;3)\ ,\ tak\ kak\ \ \vec{n}\perp \vec{s}\ \ ,\ \ \ \vec{n}\cdot \vec{s}=-3\cdot 2+2\cdot 3=0\ \ \Rightarrow \\\\l:\ \dfrac{x+1}{2}=\dfrac{y+1}{3}\ \ ,\ \ \ 3x+3=2y+2\ \ ,\ \ \boxed{\ 3x-2y+1=0\ }$