Упростить выражение ( ) 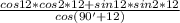
*90°
Другие вопросы по теме Математика
Популярные вопросы
- Почему вода в днепре никогда не исчезает,а в чёрном море полностью...
1 - Переделайте предложение в вопросы, ! 1)if she lives in an agricultural...
1 - 1)назовите пути биологического прогресса,регресса.объясните их смысл,...
1 - Задуманное число сначала увеличили в два с половиной раза, затем...
3 - Докажите,что образование галицко-волынского государства не было случайным...
2 - Как строение кожи при к выполняемым функциям?...
3 - Как решается это уравнение x: 100+4,57=62,8...
1 - Какое слово отличается от других по составу? 1)погоня 2) измена 3)избушка...
2 - До слів дрібний і мілкий добери слова,протилежні за значенням....
1 - Вычислите 1) 13,5*5,8-8,3*4,2-5,8*8,3+4,2*13,5 2) 5,25 в квадрате...
2
(Используем переместительный закон, чтобы изменить порядок членов. Используя cos(t+s)=cos(t)cos(s)-sin(t)sin(s), записываем выражение в развёрнутом виде) - cos12*cos2*12+sin12*sin2*12/cos(90°+12)=
(Вычисляем значение выражения используя таблицу значений тригонометрических функций или единичную окружность) - 12cos(12)cos(2)+12sin(12)sin(2)/cos(90°)cos(12)-sin(90°)sin(12)=
(Любое выражение, умноженное на 0, равно 0 и любое выражение, умноженное на 1, не изменяется) -
12cos(12)cos(2)+12sin(12)sin(2)/0cos(12)-1sin(12)=
(При добавлении или вычитании 0, величина не меняется) -
12cos(12)cos(2)+12sin(12)sin(2)/0-sin(12)/0-sin(12)=
(Используем -a/b=a/-b=- a/b, чтобы переписать дробь) -
12cos(12)cos(2)+12sin(12)sin(2)/-sin(12)=
- 12cos(12)cos(2)+12sin(12)sin(2)/sin(12)