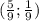[умоляю! ]
решите систему неравенств на фото!
(100) !
Другие вопросы по теме Математика
Популярные вопросы
- Через розчин, що містить 60 г сульфатної кислоти, пропустили 11,2...
3 - Мағынаны білдіретінде Түс, өкпе, ат, бас 2 сынып...
3 - с сочинением, план в закрепе, слов должно быть 150....
2 - Задачка по физике 7класс Дано F¹=20H F²=15H R-?...
2 - План к пересказу рассказа «Толстый и тонкий»...
1 - 4сынып тест қазақ тілі осжб1-нұсқа. pdf...
1 - Каким предстаёт в романе татьяны милый идеал?В чем главное обояние...
1 - ответьте на вопросы по Черчению Тема проекции...
3 - 3 - тапсырма . « Мен жұлдызнама бойынша кандай адаммын ? » тақырыбына...
3 - Выписать из трех сказок 3 предложения с качественными прилагательными...
2
Пусть x = 3k, y = 3m. Тогда
ответ: