1. Математика
  2. [умоляю! ] [80] за решение

[умоляю! ]
[80] за решение система на фото!

DashaRossgard DashaRossgard    2   10.07.2019 19:52    0

Ответы
sgerbst sgerbst  19.08.2020 08:27

Рассмотрим первое неравенство:

25x^2+25y^2+100x+100y+56\leq 0\\25x^2+100x+100+25y^2+100y+100-144\leq 0\\25(x+2)^2+25(y+2)^2\leq 144\\(x+2)^2+(y+2)^2\leq (\frac{12}{5})^2

Это круг с центром (-2; -2) и радиусом 2,4.

Рассмотрим второе неравенство:

\sqrt{x^2+4x+4+y^2+10y+25}+\sqrt{x^2+12x+36+y^2+4y+4}\leq 5\\\sqrt{(x+2)^2+(y+5)^2}+\sqrt{(x+6)^2+(y+2)^2}\leq 0

Первый корень — это расстояние от точки (-2; -5) до некоторой точки (x; y). Второй корень — это расстояние от точки (-6; -2) до этой же точки. Значит, левая часть — это сумма расстояний от точек (-2; -5) и (-6; -2) до некоторой точки. Минимальное такое расстояние — это расстояние между самими этими точками (то есть случай, когда точка лежит между известными точками) — равно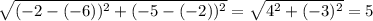 \sqrt{(-2-(-6))^2+(-5-(-2))^2}=\sqrt{4^2+(-3)^2}=5. Но по неравенству сумма расстояний не превосходит 5. Значит, оно равно 5 и задаёт множество точек, лежащих на отрезке, соединяющем точки (-2; -5) и (-6; -2) (то есть задаёт сам этот отрезок).

Найдём точки пересечения окружности и прямой, содержащей отрезок (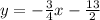y=-\frac{3}{4}x-\frac{13}{2}).

(x+2)^2+(-\frac{3}{4}x-\frac{13}{2}+2)^2=\frac{144}{25}\\(x+2)^2+(\frac{3(x+6)}{4})^2=\frac{144}{25}\\x^2+4x+4+\frac{9x^2+108x+324}{16}-\frac{144}{25}=0|*400\\400x^2+1600x+1600+225x^2+2700x+8100-2304=0\\625x^2+4300x+7396=0\\(25x+86)^2=0\\x=-\frac{86}{25}=-3.44

Решение ровно одно, значит, происходит касание. К тому же окружность касается именно отрезка, так как -6 < x < -2

y=-\frac{3}{4}*(-\frac{86}{25})-\frac{13}{2}=-\frac{98}{25}=-3.92

ответ: (-3,44; -3,92)

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Georgy0335 Georgy0335  28.05.2019 08:10
Утром петя делает в 2 раза больше звонков, чем днем, а днем - в 7 раз больше , чем вечером. во сколько раз меньше звонков петя делает вечером, чем утром?...
liyanborisova liyanborisova  28.05.2019 08:10
Сколько килограммов овощей в магазин, если огурцы составляют 27% овощей, картофель-42%, а остальные 496 кг- капуста? )...
tatarchenko04 tatarchenko04  28.05.2019 08:10
Водном рулоне 18м ткани, в другом _ 12 м ткани. на пошив комплекта постельного белья расходуется 6 м ткани. сколько комплектов белья получится из всей ткани? реши...
nasamar nasamar  28.05.2019 08:10
Сплав складається з міді, цинку і нікелю, маси яких відноситься як 4: 12: 6. яка маса всього сплаву, якщо міді і цинкку в ньому разом 320г?...
ТамараБерезанка ТамараБерезанка  28.05.2019 08:10
Вдетском лагере за одну смену израсходовали риса в 2 раза больше чем пшена,а пшена - на 24 кг меньше ,чем риса.сколько кг. пшена и риса понадобилось одной смене отдыхающих?...
AlinaGazizullina2008 AlinaGazizullina2008  28.05.2019 08:10
Сможешь ли ты без калькулятора проверить какие записи верные а какие неверные...
jdjsjsjsj jdjsjsjsj  28.05.2019 08:10
Какие приборы были незнакомые дедушке и бабушке в твоём возрасте...
Sasha2007ad Sasha2007ad  28.05.2019 08:10
Объём комнаты 75 кубических метра,высота 3 метра.найдите площадь пола комнаты....
АУЕшник2281337 АУЕшник2281337  28.05.2019 08:20
Лесные человечки раздобыли 12 мешков золота и 7 таких же мешков серебра.они пополнили свои запасы на 152 кг.сколько килограммов золота и сколько килограммов серебра...
akow08 akow08  28.05.2019 08:20
Как по татарски будет: составить диалог?...

Популярные вопросы