Математика: [умоляю! ] [50] за решение системы на фото.

[умоляю! ]
[50] за решение системы на фото.

Ответы

LeraSmile12 17.09.2020 06:28

Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: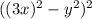 $((3x)^{2}-y^{2})^{2}$ ; В следующих двух слагаемых вынесем общий множитель "40": 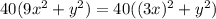$40(9x^{2}+y^{2})=40((3x)^{2}+y^{2})$ ; В итоге получим следующее уравнение: 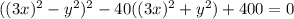$((3x)^{2}-y^{2})^{2}-40((3x)^{2}+y^{2})+400=0$ . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 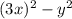$(3x)^{2}-y^{2}$ будет стоять 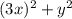$(3x)^{2}+y^{2}$ ; Это приведет к тому, что придется убавить 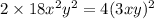$2\times 18x^2y^2=4(3xy)^{2}$ ; В итоге: 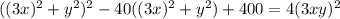$((3x)^{2}+y^{2})^{2}-40((3x)^{2}+y^{2})+400= 4(3xy)^{2}$ ; Слева стоит квадрат суммы. Уравнение примет вид: 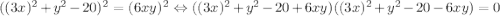$((3x)^{2}+y^{2}-20)^{2}=(6xy)^{2} \Leftrightarrow ((3x)^{2}+y^{2}-20+6xy)((3x)^{2}+y^{2}-20-6xy)=0$ ; Сворачивая еще раз: 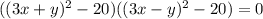$((3x+y)^{2}-20)((3x-y)^{2}-20)=0$ ; Получаем серию прямых: 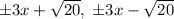$\pm 3x+\sqrt{20},\; \pm3x-\sqrt{20}$ ; А теперь приступим к рассмотрению первого уравнения.

Это уравнение задает круг с центром в точке (0, 0) и радиусом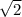 $\sqrt{2}$ ; Рассмотрим прямую 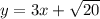$y=3x+\sqrt{20}$ ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 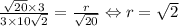$\frac{\sqrt{20}\times 3}{3\times 10\sqrt{2}}=\frac{r}{\sqrt{20}} \Leftrightarrow r=\sqrt{2}$ ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 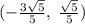$(-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5} } )$ ; Ну а все решения:

$(\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5})$