Умножение обыкновенных дробей и смешанных чисел. Урок 1 Даны два прямоугольника. Длина и ширина первого прямоугольника соответственно равны см и см, длина второго прямоугольника меньше длины первого прямоугольника на см, а ширина второго прямоугольника больше ширины первого на см. Найди периметр второго прямоугольника. ответ: см

 см

Пошаговое объяснение:

Найдем длину второго прямоугольника. По условию она меньше длины первого на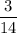  см.

 (см)  -длина второго прямоугольника .

Найдем ширину второго прямоугольника, если она больше ширины первого на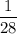  см.

(см) - ширина второго прямоугольника

Периметр прямоугольника - это сумма длин всех сторон. Периметр прямоугольника можно найти по формуле:

 где a,b- длина и ширина прямоугольника.

Значит, периметр второго прямоугольника равен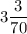  см