Укажите,если возможно,какие-либо значения a и b,при которых все члены послеловательности изображаются на координатной плоскости точками,принадлежащими полосе,ограниченной прямыми y = a и y = b , если:
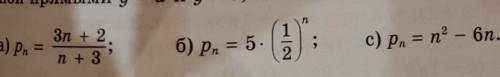
Другие вопросы по теме Математика
Популярные вопросы
- Какой плод у сложноцветные?...
3 - Назовите источники радиоизлучения во Вселенной (не менее пяти)....
3 - составить диалог в первом задании.А во втором правильно составить предложение....
3 - К 180 г 4% раствора ацетата калия добавили 120 г 6% раствора этой же соли....
3 - Поправим нужно поставить в неопределённую форму. ...
3 - УМОЛЯЮ ОЧЕНЬ Запишіть рівняння взаємодії і доберіть коефіцієнти таких...
1 - Ребят с 3 и 4 заданием,кто чем сможет!...
2 - Прочитайте высказывания В.Гюго и Е.Дворецкой о горе матери: -«Матери,...
1 - Напиши письмо-обращение к своей Родине. Начать его можно словами Л.Толстого:...
3 - Составит 10 словосочетаний на тему мой город.Составить план сочинения,каким...
1
На графике представлена последовательность a(n), где n - натуральное число. Условие задачи требует, чтобы все члены этой последовательности находились в полосе между прямыми y = a и y = b.
На графике также изображены горизонтальные прямые y = a и y = b, где a и b - искомые значения.
Для определения возможных значений a и b, нам нужно рассмотреть поведение последовательности на графике и анализировать, как меняется разность a(n+1) - a(n).
Изучим график последовательности. На графике видно, что a(1) = 1, a(2) = 2, a(3) = 1, a(4) = 0, a(5) = -1, a(6) = 0, a(7) = 1 и т.д. Можно заметить, что последовательность a(n) осциллирует между 1 и -1, исходя из формы графика и изменения разности a(n+1) - a(n).
В соответствии с условием задачи, чтобы все значения последовательности находились в полосе между прямыми y = a и y = b, нам нужно определить такие значения a и b, чтобы полоса покрывала все возможные значения последовательности.
Исходя из графика, мы видим, что наибольшее и наименьшее значение последовательности - это 1 и -1 соответственно. Исходя из этого, мы можем выбрать a = -1 и b = 1. Таким образом, все значения последовательности будут находиться в полосе между прямыми y = -1 и y = 1.
Пошаговое решение:
1. Рассматриваем график последовательности и изучаем разность a(n+1) - a(n).
2. Замечаем, что последовательность осциллирует между 1 и -1.
3. Устанавливаем значения a = -1 и b = 1.
4. Проверяем, что все значения последовательности попадают в полосу между прямыми y = -1 и y = 1.
Таким образом, при значениях a = -1 и b = 1 все члены последовательности изображаются на координатной плоскости точками, принадлежащими полосе, ограниченной прямыми y = -1 и y = 1.