Углубленная алгебра, 8 класс. Неравенства. 1. Верно ли, что если x+y≥2, то x²+y²≥2? 2. Объясните, что произойдет с величиной положительной рациональной дроби, если её числитель увеличить на 1, тогда как знаменатель - на 2. Обоснованно.
Другие вопросы по теме Математика
Популярные вопросы
- 10 вопросов к комедии горе от ума первое действие...
3 - Какие изменения происходят в хозяйстве, быту людей, в обществе?...
3 - Доказать ,что дети уязвимые слои населения...
3 - Почему санкт-петербург называется великим городом...
2 - Желке қасу,иығын көтеру,қабақ түю,бас шайқау,саусақ безеу,бас изеу,ерін шығару...
3 - Вставьте пропущенные буквы и обозначьте спряжение. 1)за двумя зайцами - ни одного...
3 - Втреугольниках abc и a1b1c1 отрезки co и c1o1 - медианы, bc = b1c1, уголb = уголb1,...
1 - Сходства и отличия между героями сказок и мифов...
3 - Решите подробно уравнение ( x-y) · (2x+y) (x-y)...
1 - Решите : выражение: 4,5-1,4 = 7,5...
2
Пошаговое объяснение:
1) Да верно. так как х+y≥2, то (x+y)^2≥4, то есть x^2+2xy+y^2≥4. Заметим, что (x-y)^2≥0, тогда x^2+y^2-2xy≥0 или x^2+y^2≥2xy. Тогда 2(x^2+y^2)≥x^2+y^2=2xy≥4 ⇒ x^2+y^2≥2
2) Вычтем старую дробь из новой: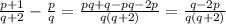 из этого мы видим, что если q>2p (дробь<1/2), то новая дробь будет больше, если q<2p (дробь >1/2), то новая дробь будет меньше, а ели q=2p (дробь =1/2), то дробь не изменится
из этого мы видим, что если q>2p (дробь<1/2), то новая дробь будет больше, если q<2p (дробь >1/2), то новая дробь будет меньше, а ели q=2p (дробь =1/2), то дробь не изменится