1. Математика
  2. У рівнобедреному трикутнику бісектриса

У рівнобедреному трикутнику бісектриса кута при основі ділить бічну сторону на відрізки 8см і 12см починаючи від вершини що протилежна основі . Знайдіть радіус кола вписаного в трикутник.(на українській )​

Макси00084322233 Макси00084322233    1   15.03.2020 07:55    4

Ответы
sidletskiy sidletskiy  11.10.2020 21:54

За властивістю бісектриси: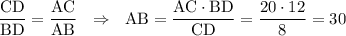 \rm \dfrac{CD}{BD}=\dfrac{AC}{AB}~~\Rightarrow~~AB=\dfrac{AC\cdot BD}{CD}=\dfrac{20\cdot 12}{8}=30

Оскільки трикутник рівнобедрений, то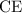 \rm CE - бісектриса, медіана і висота, то за теоремою Піфагора з трикутника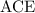 \rm ACE

\rm CE=\sqrt{AC^2-AE^2}=\sqrt{20^2-(30/2)^2}=\sqrt{175}=5\sqrt{7} см

Площа трикутника ABC:

 \rm S_{ABC}=\dfrac{1}{2}\cdot AB\cdot CE=\dfrac{1}{2}\cdot 30\cdot 5\sqrt{7}=75\sqrt{7} см²

\rm S=pr~~\Rightarrow~~~ r=\dfrac{S}{p}=\dfrac{75\sqrt{7}}{\dfrac{20+20+30}{2}}=\dfrac{75\sqrt{7}}{35}=\dfrac{15\sqrt{7}}{7} см

Відповідь: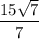 \dfrac{15\sqrt{7}}{7} см.


У рівнобедреному трикутнику бісектриса кута при основі ділить бічну сторону на відрізки 8см і 12см п
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
milana2709 milana2709  25.06.2019 12:40
Икс умножить на 5 равно 800 минус 380...
xrot xrot  25.06.2019 12:40
От пристани одновременно отчалили теплоход и катер и поплыли в одном направлении. какое расстояние будет между ними через 3 часа, если скорость теплохода 50 км/ч, а скорость...
екатерина2102 екатерина2102  25.06.2019 12:40
:на 8 одинак. халатов требуется столько же метров ткани, сколько на 6 плащей. на 1 плащ -4метра ткани. сколько метров ткани надо на один халат....
Anuliks Anuliks  25.06.2019 12:40
Краткий доклад про животноводство! 3 класс...
vtnastya05 vtnastya05  25.06.2019 12:40
Выбери верное продолжение равенства: (98+298)*65 1) 98*65+298*65. 2) 98*(298+65). 3) 98+(298*65). 4) 98*65+298...
kalabukhovalina kalabukhovalina  25.06.2019 12:40
Как из числа 167 получить 10 при исполнителя ластик, если известно что он может выполнять команды умножить на 2 стереть последнюю цифру?...
annwolf246 annwolf246  25.06.2019 12:40
А) 49 шариков раздали поровну 3 мальчикам и 4 девочкам. сколько шариков получил каждый? б) в одной коробке 9 шариков. это в 7 раз меньше, чем в другой коробке. сколько шариков...
newagain newagain  25.06.2019 12:40
На теплоходе номер билета состоит из четырёх цифр, каждый счаст- ливый билет даёт право бесплатного проезда. как узнать счастливое число или нет? берут все цифры и складывают,...
Nialya2727 Nialya2727  25.06.2019 12:40
Из одного пункта одновременно в противоположных направлениях выехали велосипедист и автомобиль.скорость велосипедиста 24 км/ч,а скорость автомобиля в 3 раза больше.на каком...
rpppppppyuv rpppppppyuv  25.06.2019 12:40
Найдите значение выражения 1 5/12: (-5/6+2/3)...

Популярные вопросы