У прямокутній системі координат ху на площині задано рівнобедренний трикутник АСВ, у якому АС=ВС , А(2:-5), В(4:3). Навколо цього трикутника описано коло, задане рівнянням (х-3)²+у²+2у=16. Визначте площу трикутника АВС.
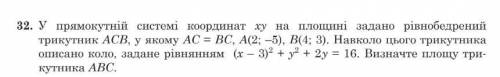
Другие вопросы по теме Математика
Популярные вопросы
- 1. Дополните структуру общественного устройства Тюркских каганатов:...
2 - Прочти ряды животных. Найди и зачеркни в каждой строке лишнее...
3 - Березкины слезы негізгі идеясы...
2 - Кто из героев говорит: «Я не хуже родом его... видали мымного...
3 - Назовите известную вам притчу, сюжет которой мы вспоминаем, читая...
2 - Это значения какой команды?...
1 - ( ) Запишіть власне визначення поняття «борець за права лю- дини»....
1 - 7 «Б» сынып оқушысы «Қазақ тілі Т2» пәнінен 1-тоқсан бойынша...
3 - Задание 3. Напишите развернутый ответ на вопрос: «Что объединяет...
1 - Какие неолитические археологические культуры на территории Казахстана...
1
В прямоугольной системе координат ху на плоскости задан равнобедренный треугольник АСВ, в котором АС=ВС , а(2:-5), в (4:3). Вокруг этого треугольника описан круг, заданное уравнением (х-3)2+у2+2у=16. Определите площадь треугольника АВС.
Пошаговое объяснение:
Найдем координаты центра окружности О из (х-3)²+у²+2у=16.
(х-3)²+(у²+2у+1)-1=16 ,
(х-3)²+(у+1)²=16+1 ,
(х-3)²+(у+1)²=17 ⇒О(3;-1) , R=√17.
Найдем координаты середины отрезка АВ , точки М( (2+4):2 :(-5+3):2 ) или М(3;-1). Ой координаты точки М и О совпали. Это означает , что это одна точка , пусть ее название О∈АВ.
R=√17, ОА=ОВ=√17 ⇒ ΔАВС-прямоугольный и катеты СА=СВ=х, АВ=2√17 .
По т. Пифагора 2х²=АВ² или 2х²=4 *17 или х=√34.
S=0.5*АС*ВС , S=0,5*√34*√34=17 (ед²)