1. Математика
  2. У=-√х у= х^3 найти площадь

У=-√х у= х^3 найти площадь с двойного интеграла. если не правильно сформулировал вопрос заранее извиняюсь

Ника65790 Ника65790    1   03.09.2019 04:00    0

Ответы
annykolis annykolis  06.10.2020 13:52
y=-\sqrt{x}\; ,\; \; y=x^3\; ,\; \; 0\leq x\leq 2

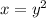 y=-\sqrt{x}  -  нижняя ветвь параболы x=y^2 , которая имеет вершину в точке (0,0) , ветви направлены вправо, проходит через точку (1,-1).
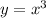 y=x^3  - кубическая парабола, проходит через точки (0,0) , (1,1) , (-1,-1).
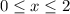 0\leq x\leq 2  - провести прямую х=2, прямая х=0 не нужна, т.к. графики кубической параболы и нижней ветви кв. параболы в точке (0,0) пересекаются.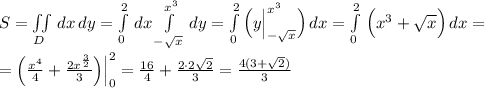

S=\iint\limits_ {D} \, dx \, dy= \int\limits^2_0 \, dx \int\limits^{x^3}_{-\sqrt{x}} \, dy= \int\limits^2_0 \Big (y\Big |_{-\sqrt{x}} ^{x^3}\Big )\, dx = \int\limits^2_0 \, \Big (x^3+\sqrt{x}\Big ) \, dx =\\\\=\Big (\frac{x^4}{4}+\frac{2x^{\frac{3}{2}}}{3}\Big )\Big |_0^2= \frac{16}{4} + \frac{2\cdot 2\sqrt2}{3} = \frac{4(3+\sqrt2)}{3}
ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Егорка8374 Егорка8374  23.07.2019 07:10
Моторной лодки скорость 22,8 км/час.скорость течения меньше скорости моторных лодок в 6 раз меньше.сколько туда струей поплывет за 3ч моторная лодка?...
Makeev20 Makeev20  23.07.2019 07:10
Как решить примеры со скобками 23+(40-3)...
DzhamalHAS DzhamalHAS  23.07.2019 07:10
Площадь прямоугольника 12м2. его длина 6м.какова ширина...
likavudu likavudu  23.07.2019 07:10
Запиши натуральные числа до 15. увеличь каждое число в 4 раза....
Novokshonovamariya Novokshonovamariya  23.07.2019 07:10
Найдите значение выражения (2 -1,5 ∙ 2,6): (- 2)....
1945269 1945269  23.07.2019 07:10
Сколько лет твоему отцу спросили у пети.он ответил так я втрое моложе папы,но зато втрое старше своей сестры,вас не и сестре вместе 50 лет.сколько лет отцу?...
alskyuq alskyuq  23.07.2019 07:10
За 8 карандашей уплатили столько же сколько за 6 ручек найдите цену карандаша и цену ручки учитывая что эти цены отличаются на 500р...
глеб380 глеб380  23.07.2019 07:10
Чему не может быть равна площадь квадрата, сторона которого выражена натуральным числом?...
MariyaPak2701 MariyaPak2701  23.07.2019 07:10
А)папа еж принес из леса двум ежатам по 9грибов.сколько грибов принес папа еж? б)каждый из 7зайчат держит 2морковки.сколько всего морковок у зайчат? в)белка разложила...
денис9645 денис9645  23.07.2019 07:10
Чему равны объем и площадь поверхности прямоуг.параллепипеда,если его длина равна 5дм4см,ширина 1дм8см,а высота 12см? ?...

Популярные вопросы