Траляля задумал целые числа b 1 , b 2 , ..., b 7 , а Труляля задумал числа a 1 , a 2 , ..., a 7 .Позжеонивыясняли,, просто числа в них взяты в разном порядке. Чётно или нечётно число (a 1 – b 1 )(a 2 – b 2 )...(a 7 – b 7 )? 4. В записи натурального числа нет девяток. Чеширский кот взял несколько последних цифр этого числа, увеличил их на 1, и сложил получившееся число с изначальным. Могло ли в сумме получится число из одних четверок? Если да - приведите пример, если нет докажите невозможность. 5. Алиса, Белая королева и Белый Кролик играют в шахматы на"вылет", то есть игрок, проигравший партию, уступает место игроку, не участвовавшему в ней. В итоге Алиса сыграла 10 партий, Белая Королева – 15, а Белый Кролик – 17. Кто из них проиграл во второй партии?
Другие вопросы по теме Математика
Популярные вопросы
- Допишите ниже предложения, заменив многоточия подходящими по...
3 - Несколько предложений художественного стиля....
2 - За 1/2 метров ткани заплатил 20 р больше чем за 1/3 такой-же...
2 - За хлеб заплатили 20 руб. а за молоко на 10 руб. больше сколько...
1 - Найдите наименьшее значение функции y=√x^2-4x+13...
3 - Что за пословица означает: жизнь постоянно меняется, так что...
1 - Напишите сочинение на тему выходной моей мечты 10 -15 предложений...
2 - Всовременном языке слово тень обладает необычайным свойством,...
2 - Что такое положение страны? какое оно у ирана?...
3 - #1 решить неравенство 1) (2x-1)/(x+2) 0 2) (14+5x)/(20-x) 0 #2...
3
Заменим набор данный набор чисел на остатки от деления на 2, которые дают числа набора. Числа у нас разбиты на пары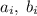 , коих всего 7. Поскольку всего чисел в наборе 7, то либо только 1, либо только 0 нечетное количество. Примем без ограничения общности, что 1 нечетное количество. Тогда найдется хотя бы одна пара
, коих всего 7. Поскольку всего чисел в наборе 7, то либо только 1, либо только 0 нечетное количество. Примем без ограничения общности, что 1 нечетное количество. Тогда найдется хотя бы одна пара 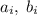 , в которой оба числа нечетны. Но в таком случае число
, в которой оба числа нечетны. Но в таком случае число  четно, и произведение четно.
четно, и произведение четно.
ответ: четно.
Пусть рассматривается число . Увеличенные на 1 некоторые последние цифры числа отличаются по четности от
. Увеличенные на 1 некоторые последние цифры числа отличаются по четности от  . Поэтому их сумма с рассматриваемым числом нечетна, значит, числа из 4 получиться не могло.
. Поэтому их сумма с рассматриваемым числом нечетна, значит, числа из 4 получиться не могло.
ответ: нет.
Посчитаем общее количество партий. Число 10+15+17=42 равно удвоенному количеству партий (поскольку, партия, сыгранная, скажем, между Кроликом и Алисой учитывается как в числе 10, так и в числе 17 ровно один раз, итого мы дважды посчитали одну и ту же партию). Значит, всего было сыграна 21 партия.
Заметим, что если игрок проигрывает все матчи, то он играет в каждой второй игре. Поэтому худший игрок сыграет хотя бы![[21/2]=10](/tpl/images/1358/1826/6f35f.png) матчей (причем 10 в том случае, если он начал играть во второй игре и проиграл). Ровно столько сыграла Алиса. Заключаем, что она начала во второй игре и проиграла все матчи. Значит, проиграла и во второй партии.
матчей (причем 10 в том случае, если он начал играть во второй игре и проиграл). Ровно столько сыграла Алиса. Заключаем, что она начала во второй игре и проиграла все матчи. Значит, проиграла и во второй партии.
ответ: Алиса