))) Только нужно решение )))
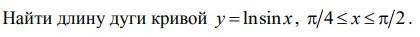
Другие вопросы по теме Математика
Популярные вопросы
- Какие бывают формы глагола в языке помню только альтернативный...
1 - Решить за 4-й класс,номер 406,автор истомина,2-я часть...
1 - 2часа автомобиль ехал со скоростью 60 километров час а следующие...
2 - Найти значение выражения tg( arccos 1/5)...
2 - Найдите число m если 60 процентов от m равны 3\7 от 42...
3 - Сколько единиц в двоичной записи восьмеричного числа 20768?...
2 - Рвхбери слова как часть речи предрассветный...
1 - Определите тему и идею ,,слепого музыканта ?...
1 - если можно чертеж построить прямоугольный треугольник по катету...
2 - Праздничные мероприятия связанные с традиционной культурой весной...
3
ответ: примерно 0,88