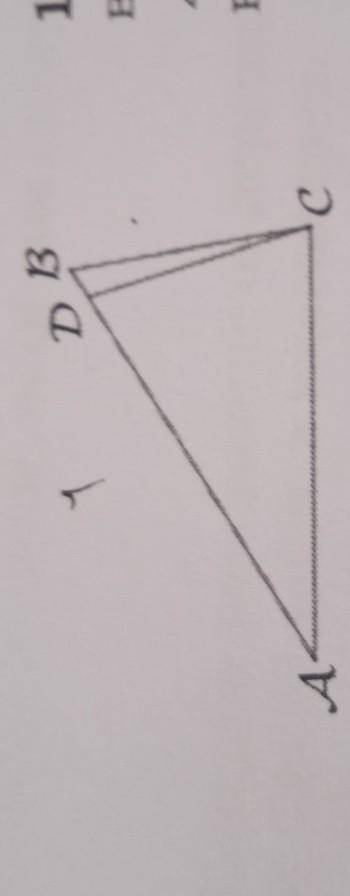
точка d на стороне ab треугольника abc выбрана так что ad равно ac известно что угол cab 32 и acb 82 найдите dbc ответ дайте в градусах​

Для решения этой задачи мы можем использовать несколько свойств треугольников.

Прежде всего, посмотрим на треугольник ABC. У нас уже заданы два угла: угол CAB равен 32 градусам, а угол ACB равен 82 градусам. Мы также знаем, что угол C равен 180 градусов (сумма углов треугольника). Теперь мы можем найти третий угол треугольника, угол B.

Угол B = 180 - угол CAB - угол ACB
Угол B = 180 - 32 - 82
Угол B = 66 градусов

Теперь мы обратим внимание на треугольники DCA и BCD. Заметим, что угол DCA равен углу CAB, так как у них общая сторона AC и сторона AD равна стороне AC. Также заметим, что угол BCD равен углу B, так как у них общая сторона BC и сторона BD равна стороне BC.

Сумма углов треугольника равна 180 градусов, поэтому мы можем записать следующее уравнение:

угол DCA + угол CAB + угол BCD = 180

Подставим известные значения:

угол CAB + 32 + угол BCD = 180

Теперь найдем угол BCD:

угол BCD = 180 - CAB - 32
угол BCD = 180 - 32 - 32
угол BCD = 116 градусов

Таким образом, угол DBC равен 116 градусам.