(tga+√3)(tgb+√3)=4
вычислите 9*((a+b)/pi)^2
Другие вопросы по теме Математика
Популярные вопросы
- Ask guestions for more information.they spent their holidays...
2 - Тело, проехав 800 м., изменило скорость с 5 м/с до 10 м/с. найти...
2 - Почему пишется фантастический а не фантостический ?...
3 - Нужны примеры предложений! 1. сочинительное (сложное предложение)...
3 - ответить на вопросы вас.это на завтра нужно. 1)өз әулеттерінде,отбасыларында...
3 - Стакан вмещает 200г молока. какую часть стакана нужно наполнить,...
1 - Как переводится это предложение? только давайте без переводчика:...
2 - Назови число которое на 5 больше 6,на 3 меньше на 11,больше 8,на...
3 - Морфологический разбор глагола думают и морфологический разбор...
2 - Дай определение терминам: 1.курганы 2.жевахова гора 3.полис 4....
1
Дано: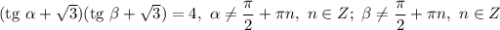
Найти: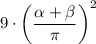
Решение. Наименьшим положительным периодом функций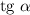 и
и 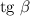 является
является 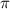 . Решим уравнение
. Решим уравнение 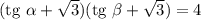 на отрезке длиной
на отрезке длиной 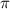 .
.
Таким образом,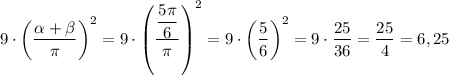
ответ: 6,25.