1. Математика
  2. [tex] \frac{ {x}^{2} - 1}{ -

\frac{ {x}^{2} - 1}{ - {x}^{2} + 4x - 5 }
решить​

doktornastia03 doktornastia03    3   29.09.2019 11:09    0

Ответы
nasty301 nasty301  09.10.2020 02:35

Я так понимаю, это сократить надо.

Числитель можно разложить по формуле разности квадратов

(a^2-b^2)=(a-b)(a+b)

(x^2-1)=(x-1)(x+1)

Знаменатель можно разложить, если корни квадратного трехчлена, найдем их:

-x^2+4x-5=0; x^2-4x+5=0; D_1=(-2)^2-5=-1

корней нет. То есть разложить не получится.

Если бы в знаменателе был, например, знак "+" перед квадратом, то тогда все было бы иначе:

$x^2+4x-5=0; a+b+c=0 \Rightarrow \left [ {{x=1} \atop {x=\frac{c}{a}=\frac{-5}{1}=-5 }} \right.

То есть по формуле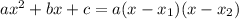 ax^2+bx+c=a(x-x_1)(x-x_2)

Получили бы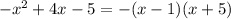 -x^2+4x-5=-(x-1)(x+5)

И дробь сократилась бы:

$\frac{(x-1)(x+1)}{-(x-1)(x+5)}=-\frac{x+1}{x+5}

Но в нашем случае не так. Тогда попробуем искусственный прием:

$\frac{x^2-1}{-x^2+4x-5}=-\frac{x^2-1}{x^2-4x+5}=-\frac{x^2-4x+5+4x-5-1}{x^2-4x+5}=

$=-\frac{x^2-4x+5+4x-6}{x^2-4x+5} =-(1+\frac{4x-6}{x^2-4x+5})=\frac{4x-6}{-x^2+4x-5}-1

Как-то так. Больше здесь ничего не сделаешь.

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
Артур15051505 Артур15051505  30.09.2019 07:50
Доклад по обж на тему «определение необходимого снаряжения для похода» заранее !...
happyga happyga  30.09.2019 07:50
Конфеты разложили в 1800ящиков по 6кг в каждый,а печенья на 6400кг больше чем конфет,разложили в ящики по 8кгв каждый.сколько кг конфет разложили в ящики по 6кг? сколько использовали...
123arrem 123arrem  30.09.2019 07:50
Відгук на твір «пісня про віщого олега»!...
Aurelli1 Aurelli1  30.09.2019 07:50
Слово с буквами чеаезинендн не хватает ещё пару букв!...
natchiy03 natchiy03  30.09.2019 07:50
Знайди целое число которое в семь раз больше за цыфру его едениц...
Васелёк05 Васелёк05  30.09.2019 07:50
Пусть а-b = с, где а b и c - натуральные числа. вставьте в окошке знак , , или , a) b □ а б) а □ с...
daaanila2015 daaanila2015  30.09.2019 07:50
3ящиках 110 кг яблок в первом на 35 кг больше чем во втором а во втором на 15 кг больше чем в третьем какова масса яблок в каждом ящике...
СофияСтепанова СофияСтепанова  30.09.2019 07:50
Слово из букв ч е н е з и е н д а составить...
Dobriyboy Dobriyboy  30.09.2019 07:50
Яку роль у житті людини відіграє байка ?...
АсяГордиенко АсяГордиенко  30.09.2019 07:50
Вычислите значение выражения 1,2 х 1 целых 5/12 + 3,6 x 2/3...

Популярные вопросы