 sin(2α), если sin(α) - cos(α)=
sin(2α), если sin(α) - cos(α)= 
Другие вопросы по теме Математика
Популярные вопросы
- З. Як хлопець — Козопасповернувся додому (Е.Андієвська «Казка про Ян»)...
2 - 1. Назовите факторы, которые обеспечивают высокие темпы роста экономики...
2 - Знайдіть висоту рівнобічної трапеції основи якої 10 і 8 см а діагональ...
2 - Два гонщика участвуют в гонках. Им предстоит проехать 98 кругов по кольцевой...
3 - Периметр треугольника равен 42 см одна строна 3/7 периметра вторая сторона...
2 - Як сталося що поранений Снап знову опинився на полюванні?Про що це свідчить...
3 - Какой характер музыкальной пьесы грига утро...
3 - Сүрет бойынша мəтін құрап жаз...
1 - Визначте кількість сторін опуклого многокутника,сума кутів якого дорівнює...
1 - ДАМ 1. Построить линейный угол двугранного угла с ребром АС, если в пирамиде...
1
Пошаговое объяснение:
sin(α) - cos(α)=
Возведем обе части в квадрат
(sin(α) - cos(α))^2=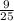
(sinα)^2 - 2*(sinα)*(cosα)+ (cosα)^2=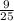
По основному тригонометрическому тождеству:
(sinα)^2+ (cosα)^2=1
Значит, имеем уравнение:
1-2*(sinα)*(cosα)=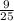
2*(sinα)*(cosα)= 1 -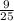
2*(sinα)*(cosα) =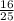
По формуле двойного угла: 2*(sinα)*(cosα)=sin(2α)
sin(2α)=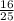
ответ: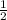 sin(2α) =
sin(2α) = 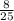
Возведем в квадрат разность
(sinα-cosα)²=9/25
sin²α-2sinα*cosα+cos²α=9/25
1-(9/25)=2sinα*cosα
(16/25):2=(sin2α)/2
(sin2α)/2=8/25