1. Математика
  2. Тема : произведение синуса и косинуса.

Тема : произведение синуса и косинуса. Задание на листке

Yaroslava1902 Yaroslava1902    2   15.04.2020 06:58    0

Ответы
ирка137 ирка137  13.10.2020 06:34

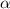\alpha +\beta =-\dfrac{\pi }{6}

Выразим \alpha:

\alpha =-\dfrac{\pi }{6}-\beta

Подставим в известное равенство:

\sin\alpha \cos\beta =\sin\left(-\dfrac{\pi }{6}-\beta\right)\cos\beta =\\\\=\dfrac{1}{2}\left(\sin\left(-\dfrac{\pi }{6}-\beta+\beta \right)+\sin\left(-\dfrac{\pi }{6}-\beta-\beta \right)\right)=\\\\=\dfrac{1}{2}\left(\sin\left(-\dfrac{\pi }{6}\right)+\sin\left(-\dfrac{\pi }{6}-2\beta \right)\right)=\dfrac{1}{2}\left(-\dfrac{1}{2}+\sin\left(-\dfrac{\pi }{6}-2\beta \right)\right)=\dfrac{1}{4}

Выразим синус:

\dfrac{1}{2}\left(-\dfrac{1}{2}+\sin\left(-\dfrac{\pi }{6}-2\beta \right)\right)=\dfrac{1}{4}

-\dfrac{1}{2}+\sin\left(-\dfrac{\pi }{6}-2\beta \right)=\dfrac{1}{2}

\sin\left(-\dfrac{\pi }{6}-2\beta \right)=1

Преобразуем искомое выражение:

4\sin(\alpha -\beta)= 4\sin\left(-\dfrac{\pi }{6}-\beta-\beta\right)=4\sin\left(-\dfrac{\pi }{6}-2\beta\right)=4\cdot1=4

ответ: 4

ПОКАЗАТЬ ОТВЕТЫ
alex13536 alex13536  13.10.2020 06:34

Дано : sinαcosβ =1/4  ; α +β = - π/6 . Найти 4sin(α +β)

- - - - - - -  

sinαcosβ =( sin(α +β) +sin(α - β) ) / 2    || *8 ||⇔

8sinαcosβ = 4sin(α +β) +4sin(α - β)

4sin(α - β) = 8sinαcosβ - 4sin(α +β) =8*1/4  - 4*sin(-π/6) =

= 2 +4*sin(π/6)  = 2 + 4*1/2 = 4 .

ПОКАЗАТЬ ОТВЕТЫ
Другие вопросы по теме Математика
danil546 danil546  01.12.2021 15:19
Скільки різних парних тризначних натуральних чисел можна скласти з цифр 1, 2, 3, 4, 5 за умови, що в кожне число кожна цифра входить не більше одного разу?...
Анёк11 Анёк11  01.12.2021 15:19
Масса стального бруска 9 кг . Из него изготовили 14 деталей масса каждой из них 5/8 кг сколько кг стали осталось?...
alekseyanci alekseyanci  01.12.2021 15:19
Перевидите 0, 1² у меня не получается ответ 0,1...
safievd6Димас safievd6Димас  01.12.2021 15:19
Преобразовать данную МКНФ в формат ДНФ f(x1, x2, x3, x4) = (x1 + x2 + x3 + x4 )(x2 + x4)(x1 + x2 + x3)(x1 + x2 + x3 )...
setkrokol setkrokol  01.12.2021 15:19
Найдите параллельную линию от 1 столбцов (если есть) к прямым линиям в столбце 2!...
Lirik1328 Lirik1328  01.12.2021 15:19
Числа x,y,z таковы, что x∈[−3,7], y∈[−2,5], z∈[−5,3]. Найдите наименьшее возможное значение величины x2+y2.Найдите наименьшее возможное значение величины xyz−z2....
зоза1 зоза1  01.12.2021 15:20
Довжина сторони правильного шестикутника дорівнює 5 см. Знайдіть довжину описаного кола....
19942424 19942424  01.12.2021 15:20
с 3 и 4 заданием буду несказанно благодарен...
zhuckovanatali1 zhuckovanatali1  01.12.2021 15:20
1. Найдите отношение 2м/26см 2. Определите расстояние на карте, если на местности оно равно 18 км, а масштаб карты равен 1 : 200 000. 3. Разделите число 60 в отношении...
martynenko5 martynenko5  01.12.2021 15:21
4) Найдите координаты точек....

Популярные вопросы